Целесообразно использовать обобщенный метод наименьших квадратов если ошибки модели

Обобщенный метод наименьших квадратов (омнк)

При несоблюдении
основных предпосылок МНК приходится
корректировать модель, изменяя ее
спецификацию, добавлять (исключать)
некоторые факторы, преобразовывать
исходные данные для того, чтобы получить
оценки коэффициентов регрессии, которые
обладают свойством несмещенности, имеют
меньшее значение дисперсии остатков и
обеспечивают в связи с этим более
эффективную статистическую проверку
значимости параметров регрессии. Этой
цели служит применение обобщенного
метода наименьших квадратов.

Обобщенный метод
наименьших квадратов применяется к
преобразованным данным и позволяет
получать оценки, которые обладают не
только свойством несмещенности, но и
имеют меньшие выборочные дисперсии.

Остановимся на
использовании ОМНК для корректировки
гетероскедастичности.

Как и раньше, будем
предполагать, что среднее значение
остаточных величин равно нулю. А вот
дисперсия их не остается неизменной
для разных значений фактора, а
пропорциональна величине
,
т.е.

, (1.35)

где
– дисперсия ошибки при конкретном-м
значении фактора;– постоянная дисперсия ошибки при
соблюдении предпосылки о гомоскедастичности
остатков;– коэффициент пропорциональности,
меняющийся с изменением величины
фактора, что и обусловливает неоднородность
дисперсии.

При этом
предполагается, что
неизвестна, а в отношении величинвыдвигаются определенные гипотезы,
характеризующие структуру
гетероскедастичности.

В общем виде для
уравнения примодель примет вид:.
В ней остаточные величины гетероскедастичны.
Предполагая в них отсутствие автокорреляции,
можно перейти к уравнению с гомоскедастичными
остатками, поделив все переменные,
зафиксированные в ходе-го
наблюдения, на.
Тогда дисперсия остатков будет величиной
постоянной, т. е..

Иными словами, от
регрессии
помы перейдем к регрессии на новых
переменных:и.
Уравнение регрессии примет вид:

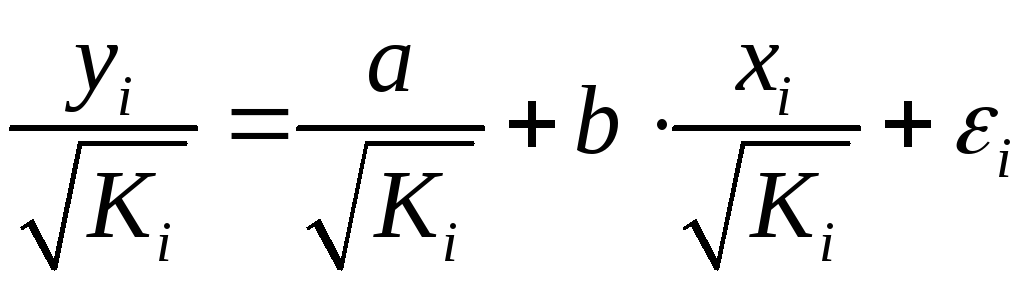, (1.36)

а исходные данные
для данного уравнения будут иметь вид:

, .

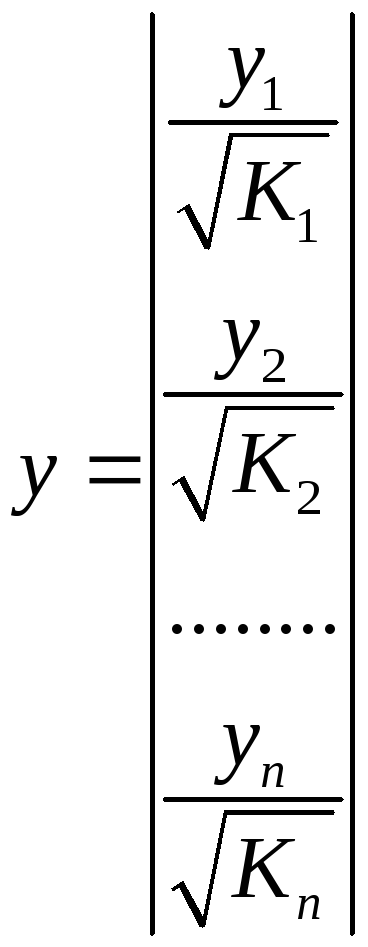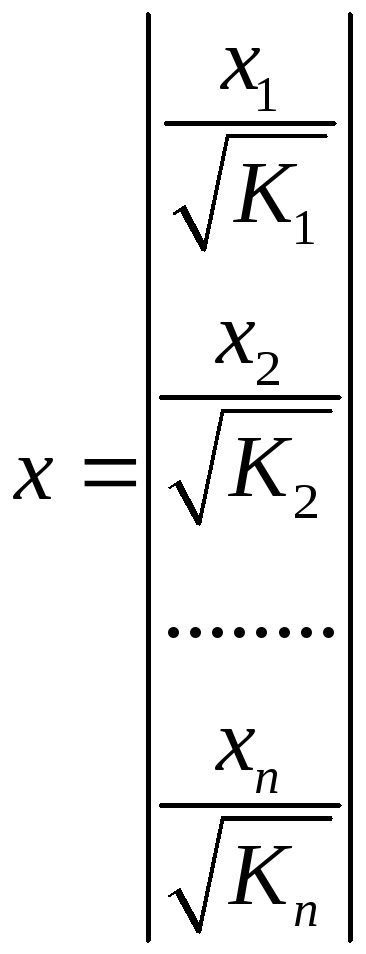По отношению к
обычной регрессии уравнение с новыми,
преобразованными переменными представляет
собой взвешенную регрессию, в которой
переменные
ивзяты с весами.

Оценка параметров
нового уравнения с преобразованными
переменными приводит к взвешенному
методу наименьших квадратов, для которого
необходимо минимизировать сумму
квадратов отклонений вида

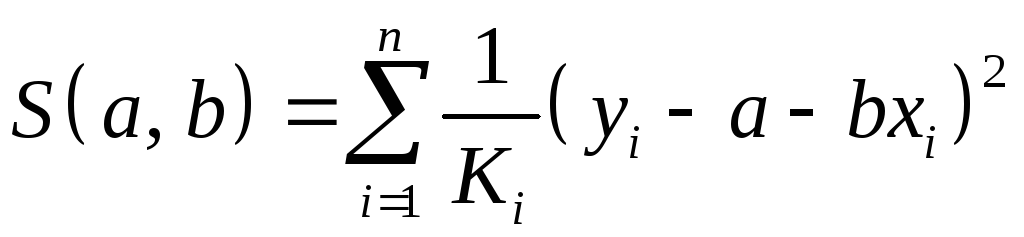. (1.37)

Соответственно
получим следующую систему нормальных
уравнений:

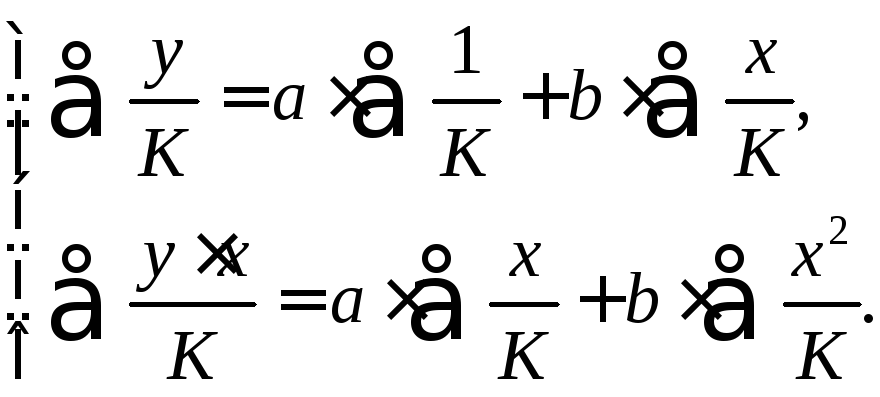
Если преобразованные
переменные
ивзять в отклонениях от средних уровней,
то коэффициент регрессииможно определить как

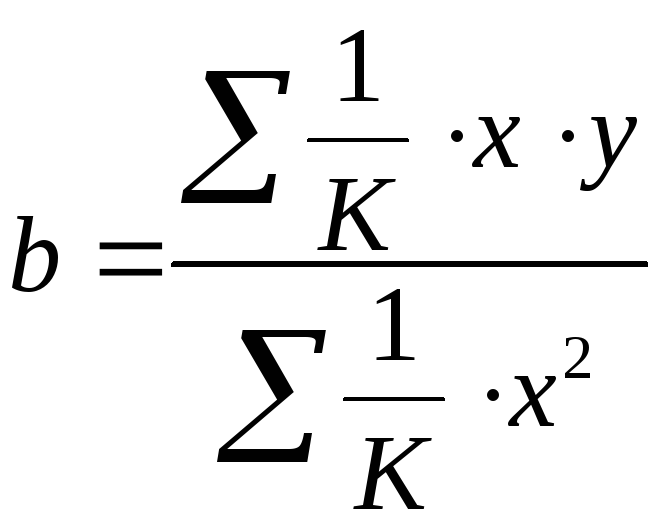. (1.38)

При обычном
применении метода наименьших квадратов
к уравнению линейной регрессии для
переменных в отклонениях от средних
уровней коэффициент регрессии
определяется по формуле:

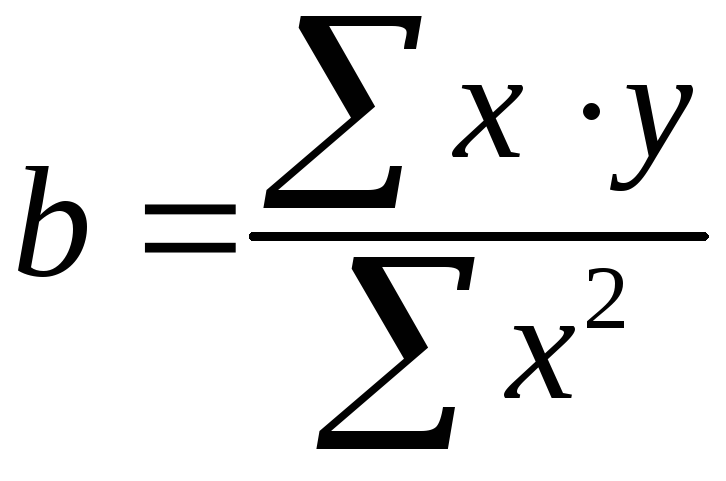. (1.39)

Как видим, при
использовании обобщенного МНК с целью
корректировки гетероскедастичности
коэффициент регрессии
представляет собой взвешенную величину
по отношению к обычному МНК с весом.

Аналогичный подход
возможен не только для уравнения парной,
но и для множественной регрессии.
Предположим, что рассматривается модель
вида

для которой
дисперсия остаточных величин оказалась
пропорциональна
.представляет собой коэффициент
пропорциональности, принимающий
различные значения для соответствующихзначений факторови.
Ввиду того, что

рассматриваемая
модель примет вид

, (1.40)

где ошибки
гетероскедастичны.

Для того чтобы
получить уравнение, где остатки
гомоскедастичны, перейдем к новым
преобразованным переменным, разделив
все члены исходного уравнения на
коэффициент пропорциональности.
Уравнение с преобразованными переменными
составит

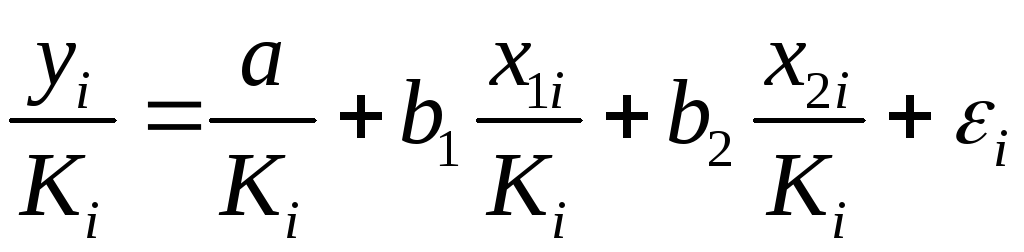. (1.41)

Это уравнение не
содержит свободного члена. Вместе с
тем, найдя переменные в новом преобразованном
виде и применяя обычный МНК к ним, получим
иную спецификацию модели:

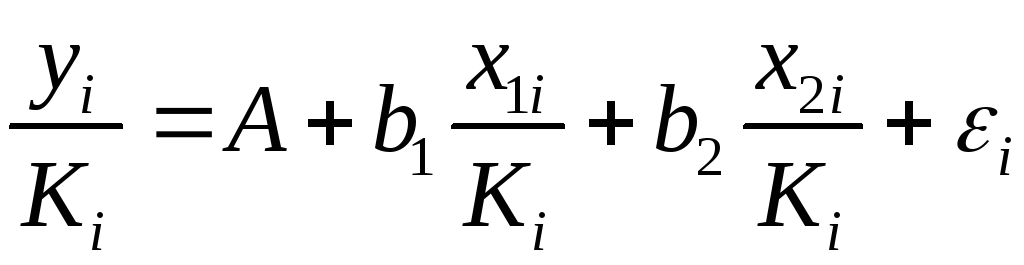. (1.42)

Параметры такой
модели зависят от концепции, принятой
для коэффициента пропорциональности
.
В эконометрических исследованиях
довольно часто выдвигается гипотеза,
что остаткипропорциональны значениям фактора.
Так, если в уравнении

предположить, что
,
т.е.и,
то обобщенный МНК предполагает оценку
параметров следующего трансформированного
уравнения:

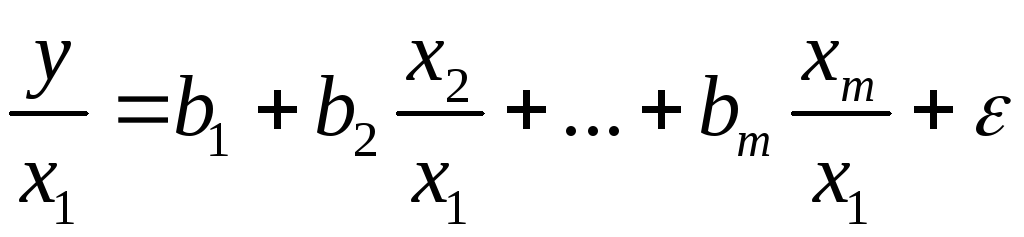. (1.43)

Применение в этом
случае обобщенного МНК приводит к тому,
что наблюдения с меньшими значениями
преобразованных переменных
имеют при определении параметров
регрессии относительно больший вес,
чем с первоначальными переменными.
Вместе с тем, следует иметь в виду, что
новые преобразованные переменные
получают новое экономическое содержание
и их регрессия имеет иной смысл, чем
регрессия по исходным данным.

Пример.Пусть– издержки производства,– объем продукции,– основные производственные фонды,– численность работников, тогда уравнение

является моделью
издержек производства с объемными
факторами. Предполагая, что
пропорциональна квадрату численности
работников,
мы получим в качестве результативного
признака затраты на одного работника,
а в качестве факторов следующие
показатели: производительность трудаи фондовооруженность труда.
Соответственно трансформированная
модель примет вид

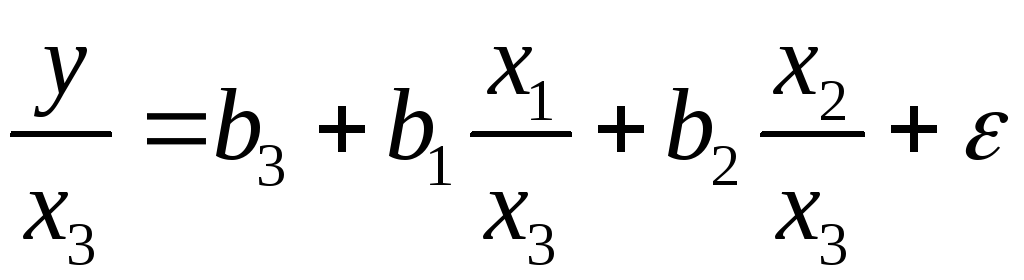где параметры
,,численно не совпадают с аналогичными
параметрами предыдущей модели. Кроме
этого, коэффициенты регрессии меняют
экономическое содержание: из показателей
силы связи, характеризующих среднее
абсолютное изменение издержек производства
с изменением абсолютной величины
соответствующего фактора на единицу,
они фиксируют при обобщенном МНК среднее
изменение затрат на работника; с
изменением производительности труда
на единицу при неизменном уровне
фовдовооруженности труда; и с изменением
фондовооруженности труда на единицу
при неизменном уровне производительности
труда.

Если предположить,
что в модели с первоначальными переменными
дисперсия остатков пропорциональна
квадрату объема продукции,
,
можно перейти к уравнению регрессии
вида

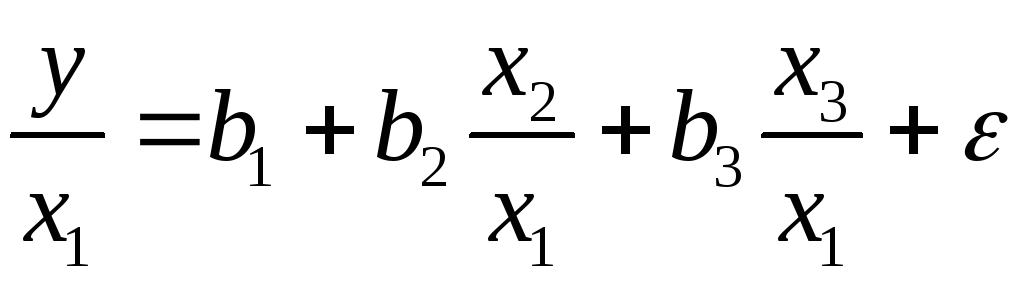В нем новые
переменные:
– затраты на единицу (или на1руб. продукции),– фондоемкость продукции,– трудоемкость продукции.

Гипотеза о
пропорциональности остатков величине
фактора может иметь реальное основание:
при обработке недостаточно однородной
совокупности, включающей как крупные,
так и мелкие предприятия, большим
объемным значениям фактора может
соответствовать большая дисперсия
результативного признака и большая
дисперсия остаточных величин.

При наличии одной
объясняющей переменной гипотеза
трансформирует линейное уравнение

в уравнение

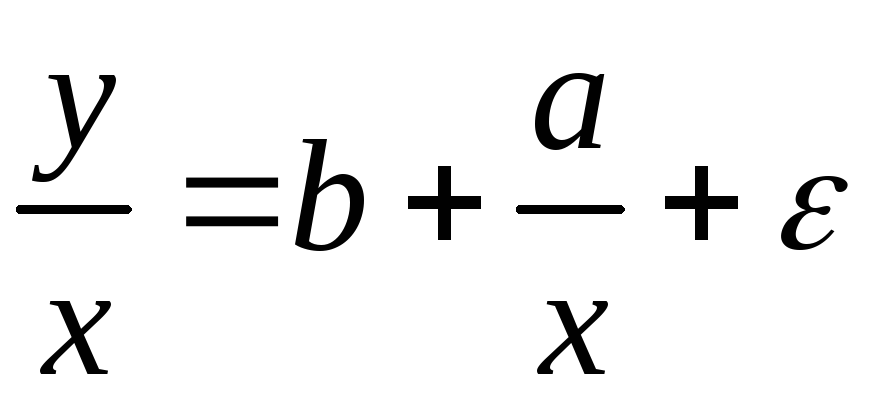в котором параметры
ипоменялись местами, константа стала
коэффициентом наклона линии регрессии,
а коэффициент регрессии – свободным
членом.

Пример.Рассматривая зависимость сбереженийот дохода,
по первоначальным данным было получено
уравнение регрессии

Применяя обобщенный
МНК к данной модели в предположении,
что ошибки пропорциональны доходу, было
получено уравнение для преобразованных
данных:

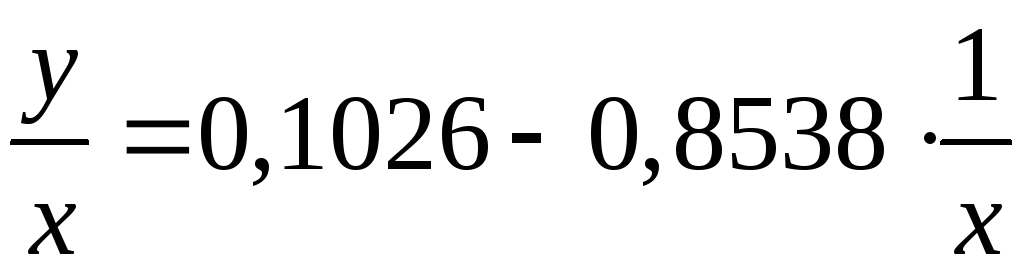Коэффициент
регрессии первого уравнения сравнивают
со свободным членом второго уравнения,
т.е. 0,1178 и 0,1026 – оценки параметра
зависимости сбережений от дохода.

Переход к
относительным величинам существенно
снижает вариацию фактора и соответственно
уменьшает дисперсию ошибки. Он представляет
собой наиболее простой случай учета
гетероскедастичности в регрессионных
моделях с помощью обобщенного МНК.
Процесс перехода к относительным
величинам может быть осложнен выдвижением
иных гипотез о пропорциональности
ошибок относительно включенных в модель
факторов. Использование той или иной
гипотезы предполагает специальные
исследования остаточных величин для
соответствующих регрессионных моделей.
Применение обобщенного МНК позволяет
получить оценки параметров модели,
обладающие меньшей дисперсией.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

Обобщённый метод наименьших квадратов (ОМНК, GLS — англ. (b) Generalized Least Squares) — метод оценки параметров регрессионных моделей (b) , являющийся обобщением классического метода наименьших квадратов (b) . Обобщённый метод наименьших квадратов сводится к минимизации «обобщённой суммы квадратов» остатков регрессии — , где — вектор остатков, — симметрическая положительно определенная (b) весовая матрица. Обычный МНК является частным случаем обобщённого, когда весовая матрица пропорциональна единичной.

Необходимо отметить, что обычно обобщённым методом наименьших квадратов называют частный случай, когда в качестве весовой матрицы используется матрица, обратная ковариационной матрице случайных ошибок модели.

Сущность обобщённого МНК

Известно, что симметрическую положительно определенную матрицу можно разложить как , где P- некоторая невырожденная квадратная матрица. Тогда обобщённая сумма квадратов может быть представлена как сумма квадратов преобразованных (с помощью P) остатков . Для линейной регрессии (b) это означает, что минимизируется величина:

где , то есть фактически суть обобщённого МНК сводится к линейному преобразованию данных и применению к этим данным обычного МНК (b) . Если в качестве весовой матрицы используется обратная ковариационная матрица (b) случайных ошибок (то есть ), преобразование P приводит к тому, что преобразованная модель удовлетворяет классическим предположениям (Гаусса-Маркова), следовательно оценки параметров с помощью обычного МНК будут наиболее эффективными в классе линейных несмещенных оценок. А поскольку параметры исходной и преобразованной модели одинаковы, то отсюда следует утверждение — оценки ОМНК являются наиболее эффективными в классе линейных несмещенных оценок (теорема Айткена). Формула обобщённого МНК имеет вид:

Ковариационная матрица этих оценок равна:

Доступный ОМНК (FGLS, Feasible GLS)

Проблема применения обобщённого МНК заключается в неизвестности ковариационной матрицы случайных ошибок. Поэтому на практике используют доступный вариант ОМНК, когда вместо V используется её некоторая оценка. Однако, и в этом случае возникает проблема: количество независимых элементов коварационной матрицы равно , где -количество наблюдений (для примера — при 100 наблюдениях нужно оценить 5050 параметров!). Следовательно, такой вариант не позволит получить качественные оценки параметров. На практике делаются дополнительные предположения о структуре ковариационной матрицы, то есть предполагается, что элементы ковариационной матрицы зависят от небольшого числа неизвестных параметров . Их количество должно быть намного меньше числа наблюдений. Сначала применяется обычный МНК, получают остатки, затем на их основе оцениваются указанные параметры . С помощью полученных оценок оценивают ковариационную матрицу ошибок и применяют обобщённый МНК с этой матрицей. В этом суть доступного ОМНК. Доказано, что при некоторых достаточно общих условиях, если оценки состоятельны, то и оценки доступного ОМНК будут состоятельны.

Взвешенный МНК

Если ковариационная матрица ошибок диагональная (имеется гетероскедастичность ошибок, но нет автокорреляции), то обобщённая сумма квадратов является фактически взвешенной суммой квадратов, где веса обратно пропорциональны дисперсиям ошибок. В этом случае говорят о взвешенном МНК (ВМНК, WLS, Weighted LS). Преобразование P в данном случае заключается в делении данных на среднеквадратическое отклонение случайных ошибок. К взвешенным таким образом данным применяется обычный МНК.

Как и в общем случае, дисперсии ошибок неизвестны и их необходимо оценить из тех же данных. Поэтому делают некоторые упрощающие предположения о структуре гетероскедастичности.

Дисперсия ошибки пропорциональна квадрату некоторой переменной

В этом случае собственно диагональными элементами являются величины, пропорциональные этой переменной (обозначим её Z) . Причем коэффициент пропорциональности не нужен для оценки. Поэтому фактически процедура в данном случае следующая: разделить все переменные на Z (включая константу, то есть появится новая переменная 1/Z). Причем Z может быть одной из переменных самой исходной модели (в этом случае в преобразованной будет константа). К преобразованным данным применяется обычный МНК для получения оценок параметров:

Однородные группы наблюдений

Пусть имеется n наблюдений разбитых на m однородных групп, внутри каждой из которых предполагается одинаковая дисперсия. В этом случае сначала модель оценивают обычным МНК и находят остатки. По остаткам внутри каждой группы оценивают дисперсии ошибок групп как отношение сумм квадратов остатков к количеству наблюдений в группе. Далее данные каждой j-й группы наблюдений делятся на и к преобразованным подобным образом данным применяется обычный МНК для оценки параметров.

ОМНК в случае автокорреляции

Если случайные ошибки подчиняются AR(1) модели , то без учета первого наблюдения преобразование P будет заключаться в следующем: из текущего значения переменных отнимаются предыдущие, умноженные на :

Данное преобразование называется авторегрессионным преобразованием. Для первого наблюдения применяется поправка Прайса — Уинстена — данные первого наблюдения умножаются на . Случайная ошибка преобразованной модели равна , которая по предположению есть белый шум. Следовательно применение обычного МНК позволит получить качественные оценки такой модели.

Поскольку коэффициент авторегрессии неизвестен, то применяются различные процедуры доступного ОМНК.

Процедура Кохрейна-Оркатта

Шаг 1. Оценка исходной модели методом наименьших квадратов (b) и получение остатков модели.

Шаг 2. Оценка коэффициента автокорреляции остатков модели (формально её можно получить также как МНК-оценку параметра авторегрессии во вспомогательной регрессии остатков )

Шаг 3. Авторегрессионное преобразование данных (с помощью оцененного на втором шаге коэффициента автокорреляции) и оценка параметров преобразованной модели обычным МНК.

Оценки параметров преобразованной модели и являются оценками параметров исходной модели, за исключением константы, которая восстанавливается делением константы преобразованной модели на 1-r. Процедура может повторяться со второго шага до достижения требуемой точности.

Процедура Хилдрета — Лу

В данной процедуре производится прямой поиск значения коэффициента автокорреляции, которое минимизирует сумму квадратов остатков преобразованной модели. А именно задаются значения r из возможного интервала (-1;1) с некоторым шагом. Для каждого из них производится авторегрессионное преобразование, оценивается модель обычным МНК и находится сумма квадратов остатков. Выбирается тот коэффициент автокорреляции, для которого эта сумма квадратов минимальна. Далее в окрестности найденной точки строится сетка с более мелким шагом и процедура повторяется заново.

Процедура Дарбина

Преобразованная модель имеет вид:

Раскрыв скобки и перенеся лаговую зависимую переменную вправо получаем

Введем обозначения . Тогда имеем следующую модель

Данную модель необходимо оценить с помощью обычного МНК. Тогда коэффициенты исходной модели восстанавливаются как .

При этом полученная оценка коэффициента автокорреляции (b) может быть использована для авторегрессионного преобразования и применения МНК для этой преобразованной модели для получения более точных оценок параметров.

См. также

Метод наименьших квадратов (b)

Литература

Магнус Я. Р., Катышев П. К., Пересецкий А. А. Эконометрика. Начальный курс . — 2004.

Источник

При нарушении гомоскедастичности и наличии автокорреляции ошибок рекомендуется традиционный метод наименьших квадратов (известный в английской терминологии как метод OLS – Ordinary Least Squares) заменять Обобщенным методом, т. е. Методом GLS (Generalized Least Squares).

Обобщенный метод наименьших квадратов применяется к преобразованным данным и позволяет получать оценки, которые обладают не только свойством несмещенности, но и имеют меньшие выборочные дисперсии. Рассмотрим использование ОМНК для корректировки гетероскедастичности.

Будем предполагать, что среднее значение остаточных величин равно нулю. А вот дисперсия их не остается неизменной для разных значений фактора, а пропорциональна величине , т. е.

Где – дисперсия ошибки при конкретном I-м значении фактора; – постоянная дисперсия ошибки при соблюдении предпосылки о гомоскедастичности остатков; – коэффициент пропорциональности, меняющийся с изменением величины фактора, что и обусловливает неоднородность дисперсии.

При этом предполагается, что неизвестна, а в отношении величин выдвигаются определенные гипотезы, характеризующие структуру гетероскедастичности.

В общем виде для уравнения при модель примет вид: . В ней остаточные величины гетероскедастичны. Предполагая в них отсутствие автокорреляции, можно перейти к уравнению с гомоскедастичными остатками, поделив все переменные, зафиксированные в ходе I-го наблюдения, на . Тогда дисперсия остатков будет величиной постоянной, т. е. .

Иными словами, от регрессии Y по X мы перейдем к регрессии на новых переменных: и . Уравнение регрессии примет вид:

А исходные данные для данного уравнения будут иметь вид:

, .

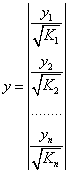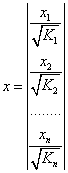По отношению к обычной регрессии уравнение с новыми, преобразованными переменными представляет собой взвешенную регрессию, в которой переменные Y и X взяты с весами .

Оценка параметров нового уравнения с преобразованными переменными приводит к взвешенному методу наименьших квадратов, для которого необходимо минимизировать сумму квадратов отклонений вида

Соответственно получим следующую систему нормальных уравнений:

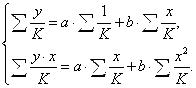
Если преобразованные переменные X и Y взять в отклонениях от средних уровней, то коэффициент регрессии B можно определить как

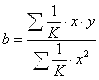При обычном применении метода наименьших квадратов к уравнению линейной регрессии для переменных в отклонениях от средних уровней коэффициент регрессии B определяется по формуле:

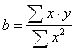Как видим, при использовании обобщенного МНК с целью корректировки гетероскедастичности коэффициент регрессии B представляет собой взвешенную величину по отношению к обычному МНК с весом .

Аналогичный подход возможен не только для уравнения парной, но и для множественной регрессии. Предположим, что рассматривается модель вида

Для которой дисперсия остаточных величин оказалась пропорциональна . представляет собой коэффициент пропорциональности, принимающий различные значения для соответствующих I значений факторов и . Ввиду того, что

Рассматриваемая модель примет вид

Где ошибки гетероскедастичны.

Для того чтобы получить уравнение, где остатки гомоскедастичны, перейдем к новым преобразованным переменным, разделив все члены исходного уравнения на коэффициент пропорциональности K. Уравнение с преобразованными переменными составит

Это уравнение не содержит свободного члена. Вместе с тем, найдя переменные в новом преобразованном виде и применяя обычный МНК к ним, получим иную спецификацию модели:

Параметры такой модели зависят от концепции, принятой для коэффициента пропорциональности . В эконометрических исследованиях довольно часто выдвигается гипотеза, что остатки пропорциональны значениям фактора. Так, если в уравнении

Предположить, что , т. е. и , то обобщенный МНК предполагает оценку параметров следующего трансформированного уравнения:

Применение в этом случае обобщенного МНК приводит к тому, что наблюдения с меньшими значениями преобразованных переменных имеют при определении параметров регрессии относительно больший вес, чем с первоначальными переменными. Вместе с тем, следует иметь в виду, что новые преобразованные переменные получают новое экономическое содержание и их регрессия имеет иной смысл, чем регрессия по исходным данным.

Пример. Пусть Y – издержки производства, – объем продукции, – основные производственные фонды, – численность работников, тогда уравнение

Является моделью издержек производства с объемными факторами. Предполагая, что пропорциональна квадрату численности работников , мы получим в качестве результирующего показателя затраты на одного работника , а в качестве факторов следующие показатели: производительность труда и фондовооруженность труда . Соответственно трансформированная модель примет вид

Где параметры , , численно не совпадают с аналогичными параметрами предыдущей модели. Кроме этого, коэффициенты регрессии меняют экономическое содержание: из показателей силы связи, характеризующих среднее абсолютное изменение издержек производства с изменением абсолютной величины соответствующего фактора на единицу, они фиксируют при обобщенном МНК среднее изменение затрат на работника; с изменением производительности труда на единицу при неизменном уровне фондовооруженности труда; и с изменением фондовооруженности труда на единицу при неизменном уровне производительности труда.

Если предположить, что в модели с первоначальными переменными дисперсия остатков пропорциональна квадрату объема продукции, , можно перейти к уравнению регрессии вида

В нем новые переменные: – затраты на единицу (или на 1 руб. продукции), – фондоемкость продукции, – трудоемкость продукции.

Гипотеза о пропорциональности остатков величине фактора может иметь реальное обоснование: при обработке недостаточно однородной совокупности, включающей как крупные, так и мелкие предприятия, большим объемным значениям фактора может соответствовать большая дисперсия результативного признака и большая дисперсия остаточных величин.

При наличии одной объясняющей переменной гипотеза трансформирует линейное уравнение

В уравнение

В котором параметры A и B поменялись местами, константа стала коэффициентом наклона линии регрессии, а коэффициент регрессии – свободным членом.

Пример. Рассматривая зависимость сбережений Y от дохода X, по первоначальным данным было получено уравнение регрессии

Применяя обобщенный МНК к данной модели в предположении, что ошибки пропорциональны доходу, было получено уравнение для преобразованных данных:

Коэффициент регрессии первого уравнения сравнивают со свободным членом второго уравнения, т. е. 0,1178 и 0,1026 – оценки параметра B зависимости сбережений от дохода.

Переход к относительным величинам существенно снижает вариацию фактора и соответственно уменьшает дисперсию ошибки. Он представляет собой наиболее простой случай учета гетероскедастичности в регрессионных моделях с помощью обобщенного МНК. Применение обобщенного МНК позволяет получить оценки параметров модели, обладающие меньшей дисперсией.

< Предыдущая		Следующая >

Источник

В предыдущих параграфах данной главы мы рассматривали случай отказа от одной предпосылки классической линейной модели множественной регрессии. Теперь мы расширим наш анализ и откажемся сразу от двух предпосылок: от предпосылок №№4-5 (о постоянстве дисперсии случайной ошибки и о некоррелированности разных случайных ошибок между собой). В техническом смысле этот параграф несколько сложнее предыдущих (в частности, тут более широко используется линейная алгебра). Поэтому, если вы заинтересованы в том, чтобы разобраться только в прикладных аспектах множественной регрессии, а в соответствующих вычислениях готовы полностью довериться эконометрическому пакету, можете его пропустить.

Отказ от указанных двух предпосылок означает, что ковариационная матрица вектора случайных ошибок (таблица, в которой записаны все ковариации между (varepsilon_{i}) и (varepsilon_{j}), см. параграф 3.3) больше не является диагональной матрицей с одинаковыми числами на главной диагонали, как это было в первоначальной классической модели. Теперь ковариационная матрица вектора случайных ошибок Ω — это произвольная ковариационная матрица (разумеется, так как это не совсем любая матрица, а именно ковариационная матрица, то по своим свойствам она является симметричной и положительно определенной).

Модель, в которой сохранены только первые три предпосылки классической линейной модели множественной регрессии, называется обобщенной линейной моделью множественной регрессии.

Проанализируем, к каким последствиям приводит отказ от предпосылок №№4-5.

Во-первых, полученная обычным методом наименьших квадратов оценка ({widehat{beta} = left( {X^{‘}X} right)^{- 1}}X’y) остается несмещенной (это свойство мы доказывали, опираясь как раз лишь на первые три предпосылки).

Во-вторых, МНК-оценки хоть и остаются несмещенными, но больше не являются эффективными.

В-третьих, если мы оцениваем ковариационную матрицу вектора оценок коэффициентов (которая нужна для тестирования всевозможных гипотез), то оценка (widehat{V}{{(widehat{beta})} = left( {X^{‘}X} right)^{- 1}}S^{2}) смещена и больше не является корректной.

Чтобы убедиться в этом, посчитаем ковариационную матрицу от (widehat{beta}) в условиях обобщенной модели (при этом мы используем свойства ковариационной матрицы, перечисленные в параграфе 3.3):

(V{left( widehat{beta} right) = V}{leftlbrack {{({X^{‘}X})}^{- 1}X’y} rightrbrack = V}{leftlbrack {{({X^{‘}X})}^{- 1}X'{({mathit{Xbeta} + varepsilon})}} rightrbrack =})

({}V{leftlbrack {{({{({X^{‘}X})}^{- 1}X’})}varepsilon} rightrbrack = left( {X^{‘}X} right)^{- 1}}X^{‘}Vlbrackvarepsilonrbrack{left( {left( {X^{‘}X} right)^{- 1}X^{‘}} right)^{‘} = {({X^{‘}X})}^{- 1}}X^{‘}Omega{left( {left( {X^{‘}X} right)^{- 1}X^{‘}} right)^{‘} = {({X^{‘}X})}^{- 1}}X^{‘}Omega X{({X^{‘}X})}^{- 1})

Так выглядит ковариационная матрица вектора МНК-оценок в обобщенной модели. Ясно, что она не может быть корректно оценена стандартной оценкой (left( {X^{‘}X} right)^{- 1}S^{2}). Следовательно, прежней формулой пользоваться нельзя: если мы будем использовать стандартные ошибки, рассчитанные по обычной формуле (предполагая выполнение предпосылок классической линейной модели), то получим некорректные стандартные ошибки, что может привести нас к неверным выводам по поводу значимости или незначимости тех или иных регрессоров.

Таким образом, последствия перехода к обобщенной модели аналогичны тем, что мы наблюдали для случая гетероскедастичности. Это неудивительно, так как гетероскедастичность — частный случай обобщенной линейной модели.

Поэтому для получения эффективных оценок обычный МНК не подойдет, и придется воспользоваться альтернативным методом — обобщенным МНК (ОМНК, generalized least squares, GLS). Формулу для расчета оценок коэффициентов при помощи ОМНК позволяет получить специальная теорема.

Теорема Айткена

Если

модель линейна по параметрам и правильно специфицирована
({y = {mathit{Xbeta} + varepsilon}},)
матрица Х — детерминированная матрица, имеющая максимальный ранг k,
(E{(varepsilon) = overrightarrow{0}}),
(V{(varepsilon) = Omega}) — произвольная положительно определенная и симметричная матрица,

то оценка вектора коэффициентов модели ({{widehat{beta}}^{} = {({X’Omega^{- 1}X})}^{- 1}}X’Omega^{- 1}y) является:

несмещенной
и эффективной, то есть имеет наименьшую ковариационную матрицу в классе всех несмещенных и линейных по y оценок.

Предпосылки теоремы Айткена — это предпосылки обобщенной линейной модели множественной регрессии. Из них первые три — стандартные, как в классической модели, а четвертая ничего особого не требует (у вектора случайных ошибок может быть любая ковариационная матрица без каких-либо дополнительных специальных ограничений). Сама теорема Айткена является аналогом теоремы Гаусса — Маркова для случая обобщенной модели.

Докажем эту теорему.

Из линейной алгебры известно: если матрица (Omega) симметрична и положительно определена, то существует такая матрица P, что

(P’bullet{P = Omega^{- 1}}) ⇔ ({P^{‘} = Omega^{- 1}}bullet P^{- 1})

А раз такое представление возможно, то воспользуемся им для замены переменных. От вектора значений зависимой переменной (y), перейдем к вектору (Pbullet y), обозначив его как вектор ({y^{} = P}bullet y). Аналогичным образом введем матрицу ({X^{} = P}bullet X) и вектор ошибок ({varepsilon^{} = P}bulletvarepsilon).

Вернемся к исходной модели, параметры которой нас и интересуют:

({y = X}{beta + varepsilon})

Умножим левую и правую части равенства на матрицу (P):

({mathit{Py} = mathit{PX}}{beta + mathit{Pvarepsilon}})

С учетом новых обозначений это равенство можно записать так:

({y^{} = X^{}}{beta + varepsilon^{}})

Для новой модели (со звездочками) выполняются предпосылки теоремы Гаусса-Маркова. Чтобы в этом убедиться, достаточно показать, что математическое ожидание вектора случайных ошибок является нулевым вектором (третья предпосылка классической модели) и ковариационная матрица вектора случайных ошибок является диагональной с одинаковыми элементами на главной диагонали (четвертая и пятая предпосылки).

Для этого вычислим математическое ожидание нового вектора ошибок:

(E{left( varepsilon^{} right) = E}{left( mathit{Pvarepsilon} right) = P}bullet E{(varepsilon) = P}bullet{overrightarrow{0} = overrightarrow{0}})

Теперь вычислим ковариационную матрицу вектора (varepsilon^{}):

(V{left( varepsilon^{} right) = V}{left( {Pbulletvarepsilon} right) = P}bullet V(varepsilon)bullet{P^{‘} = P}bulletOmegabullet{P^{‘} = P}bulletOmegabulletOmega^{- 1}bullet{P^{- 1} = I_{n}})

Здесь (I_{n}) обозначает единичную матрицу размера n на n.

Следовательно, для модели со звездочками выполняются все предпосылки теоремы Гаусса — Маркова. Поэтому получить несмещенную и эффективную оценку вектора коэффициентов можно, применив к этой измененной модели обычный МНК:

({{widehat{beta}}^{} = left( {{X^{}}^{‘}X^{}} right)^{- 1}}{X^{}}^{‘}y^{})

Теперь осталось вернуться к исходным обозначениям, чтобы получить формулу несмещенной и эффективной оценки интересующего нас вектора в терминах обобщенной модели:

({{widehat{beta}}^{} = left( {{X^{}}^{‘}X^{}} right)^{- 1}}{X^{}}^{‘}{y^{} = left( {{(mathit{PX})}^{‘}mathit{PX}} right)^{- 1}}left( mathit{PX} right)^{‘}{mathit{Py} = left( {X’P’mathit{PX}} right)^{- 1}}X^{‘}P^{‘}{mathit{Py} =}left( {X’Omega^{- 1}P^{- 1}mathit{PX}} right)^{- 1}X’Omega^{- 1}P^{- 1}{mathit{Py} = {({X’Omega^{- 1}X})}^{- 1}}X’Omega^{- 1}y)

Что и требовалось доказать.

Взвешенный МНК, который мы обсуждали ранее, — это частный вариант обобщенного МНК (для случая, когда только предпосылка №4 нарушена, а предпосылка №5 сохраняется).

Как и при использовании взвешенного МНК в ситуации применения ОМНК коэффициент R-квадрат не обязан лежать между нулем и единицей и не может быть интерпретирован стандартным образом.

Слабая сторона ОМНК состоит в том, что для его реализации нужно знать не только матрицу регрессоров X с вектором значений зависимой переменной y, но и ковариационную матрицу вектора случайных ошибок (Omega). На практике, однако, эта матрица почти никогда не известна. Поэтому в прикладных исследованиях практически всегда вместо ОМНК используется, так называемый, доступный ОМНК (его ещё называют практически реализуемый ОМНК, feasible GLS). Идея доступного ОМНК состоит в том, что следует сначала оценить матрицу (Omega) (традиционно обозначим её оценку (widehat{Omega})), а уже затем получить оценку вектора коэффициентов модели, заменив в формуле ОМНК (Omega) на (widehat{Omega}):

({{widehat{beta}}^{} = {({X'{widehat{Omega}}^{- 1}X})}^{- 1}}X'{widehat{Omega}}^{- 1}y.)

Применение этого подхода осложняется тем, что (widehat{Omega}) не может быть оценена непосредственно без дополнительных предпосылок, так как в ней слишком много неизвестных элементов. Действительно, в матрице размер (n) на (n) всего (n^{2}) элементов, и оценить их все, имея всего (n) наблюдений, представляется слишком амбициозной задачей. Даже если воспользоваться тем, что матрица (Omega) является симметричной, в результате чего достаточно оценить только элементы на главной диагонали и над ней, мы все равно столкнемся с необходимостью оценивать (left( {n + 1} right){n/2}) элементов, что всегда больше числа доступных нам наблюдений.

Поэтому процедура доступного ОМНК устроена так:

Делаются некоторые предпосылки по поводу того, как устроена ковариационная матрица вектора случайных ошибок (Omega). На основе этих предпосылок оценивается матрица (widehat{Omega}).
После этого по формуле ({({X'{widehat{Omega}}^{- 1}X})}^{- 1}X'{widehat{Omega}}^{- 1}y) вычисляется вектор оценок коэффициентов модели.

Из сказанного следует, что доступный ОМНК может быть реализован только в ситуации, когда есть разумные основания сформулировать те или иные предпосылки по поводу матрицы (widehat{Omega}). Рассмотрим некоторые примеры таких ситуаций.

Пример 5.4. Автокорреляция и ОМНК-оценка

Рассмотрим линейную модель ({y = X}{beta + varepsilon}), для которой дисперсия случайных ошибок постоянна, однако наблюдается так называемая автокорреляция первого порядка:

(varepsilon_{i} = {{rho ast varepsilon_{i — 1}} + u_{i}})

Здесь (u_{i}) — независимые и одинаково распределенные случайные величины с дисперсией (sigma_{u}^{2}), а (rhoin{({{- 1},1})}) — коэффициент автокорреляции.

(а) Найдите ковариационную матрицу вектора случайных ошибок для представленной модели.

(б) Запишите в явном виде формулу ОМНК-оценки вектора коэффициентов модели, предполагая, что коэффициент (rho) известен.

Примечание: в отличие от гетероскедастичности, автокорреляция случайных ошибок обычно наблюдается не в пространственных данных, а во временных рядах. Для временных рядов вполне естественна подобная связь будущих случайных ошибок с предыдущими их значениями.

Решение:

(а) Используя условие о постоянстве дисперсии случайной ошибки, то есть условие (mathit{var}{{(varepsilon_{i})} = mathit{var}}{(varepsilon_{i — 1})}), найдем эту дисперсию:

(mathit{var}{{(varepsilon_{i})} = mathit{var}}{({{rho ast varepsilon_{i — 1}} + u_{i}})})

(mathit{var}{{(varepsilon_{i})} = rho^{2}}mathit{var}{{(varepsilon_{i — 1})} + mathit{var}}{(u_{i})})

(mathit{var}{{(varepsilon_{i})} = rho^{2}}mathit{var}{{(varepsilon_{i})} + sigma_{u}^{2}})

(mathit{var}{left( varepsilon_{i} right) = frac{sigma_{u}^{2}}{1 — rho^{2}}}.)

Тем самым мы нашли элементы, которые будут стоять на главной диагонали ковариационной матрицы вектора случайных ошибок. Теперь найдем элементы, которые будут находиться непосредственно на соседних с главной диагональю клетках:

(mathit{cov}{left( {varepsilon_{i},varepsilon_{i — 1}} right) = mathit{cov}}{left( {{{rho ast varepsilon_{i — 1}} + u_{i}},varepsilon_{i — 1}} right) = {rho ast mathit{cov}}}{left( {varepsilon_{i — 1},varepsilon_{i — 1}} right) + mathit{cov}}{left( {u_{i},varepsilon_{i — 1}} right) = {rho ast mathit{var}}}{{left( varepsilon_{i — 1} right) + 0} = frac{rho ast sigma_{u}^{2}}{1 — rho^{2}}})

По аналогии легко убедиться, что

(mathit{cov}{left( {varepsilon_{i},varepsilon_{i — k}} right) = frac{rho^{k} ast sigma_{u}^{2}}{1 — rho^{2}} = frac{sigma_{u}^{2} ast rho^{k}}{1 — rho^{2}}}.)

Следовательно, ковариационная матрица вектора случайных ошибок имеет вид:

({Omega = frac{sigma_{u}^{2}}{1 — rho^{2}}}begin{pmatrix} begin{matrix} 1 & rho \ rho & 1 \ end{matrix} & ldots & begin{matrix} rho^{n — 2} & rho^{n — 1} \ rho^{n — 3} & rho^{n — 2} \ end{matrix} \ ldots & ldots & ldots \ begin{matrix} rho^{n — 2} & rho^{n — 3} \ rho^{n — 1} & rho^{n — 2} \ end{matrix} & ldots & begin{matrix} 1 & rho \ rho & 1 \ end{matrix} \ end{pmatrix})

(б) Вектор ОМНК-оценок коэффициентов имеет вид:

({{widehat{beta}}^{} = {({X’Omega^{- 1}X})}^{- 1}}X^{‘}Omega^{- 1}{y =}{left( {X’begin{pmatrix} begin{matrix} 1 & rho \ rho & 1 \ end{matrix} & ldots & begin{matrix} rho^{n — 2} & rho^{n — 1} \ rho^{n — 3} & rho^{n — 2} \ end{matrix} \ ldots & ldots & ldots \ begin{matrix} rho^{n — 2} & rho^{n — 3} \ rho^{n — 1} & rho^{n — 2} \ end{matrix} & ldots & begin{matrix} 1 & rho \ rho & 1 \ end{matrix} \ end{pmatrix}^{- 1}X} right)^{- 1} ast}X’begin{pmatrix} begin{matrix} 1 & rho \ rho & 1 \ end{matrix} & ldots & begin{matrix} rho^{n — 2} & rho^{n — 1} \ rho^{n — 3} & rho^{n — 2} \ end{matrix} \ ldots & ldots & ldots \ begin{matrix} rho^{n — 2} & rho^{n — 3} \ rho^{n — 1} & rho^{n — 2} \ end{matrix} & ldots & begin{matrix} 1 & rho \ rho & 1 \ end{matrix} \ end{pmatrix}^{- 1}y)

Обратите внимание, что дробь (frac{sigma_{u}^{2}}{1 — rho^{2}}) при расчете представленной оценки сокращается. Поэтому для вычисления оценки знать величину (sigma_{u}^{2}) не нужно.

Примечание: если коэффициент автокорреляции (rho) неизвестен, то его можно легко оценить. Например, для этого можно применить обычный МНК к исходной регрессии, получить вектор остатков и оценить регрессию ({widehat{e}}_{i} = {widehat{rho} ast e_{i — 1}}). Полученной оценки (widehat{rho}) достаточно, чтобы вычислить ОМНК-оценку вектора параметров модели. Тем самым в представленном примере для применения доступного ОМНК достаточно оценить всего один параметр ковариационной матрицы вектора оценок коэффициентов.

Пример 5.5. Гетероскедастичность и ОМНК-оценка

Рассмотрим линейную модель ({y = X}{beta + varepsilon}), для которой выполнены все предпосылки классической линейной модели множественной регрессии за одним исключением: дисперсия случайной ошибки прямо пропорциональна квадрату некоторой известной переменной

(mathit{var}{left( varepsilon_{i} right) = sigma_{i}^{2} = sigma_{0}^{2}}{z_{i}^{2} > 0}.)

(а) Найдите ковариационную матрицу вектора случайных ошибок для представленной модели.

(б) Запишите в явном виде формулу ОМНК-оценки вектора коэффициентов модели.

Решение:

(а) Так как в этом случае нарушена только четвертая предпосылка классической линейной модели множественной регрессии, то вне главной диагонали ковариационной матрицы вектора случайных ошибок будут стоять нули.

(Omega = begin{pmatrix} begin{matrix} {sigma_{0}^{2}z_{1}^{2}} & 0 \ 0 & {sigma_{0}^{2}z_{2}^{2}} \ end{matrix} & begin{matrix} ldots & 0 \ ldots & 0 \ end{matrix} \ begin{matrix} ldots & ldots \ 0 & 0 \ end{matrix} & begin{matrix} ldots & ldots \ ldots & {sigma_{0}^{2}z_{n}^{2}} \ end{matrix} \ end{pmatrix})

(б) Обратите внимание, что при подстановке в общую формулу для ОМНК-оценки величина (sigma_{0}^{2}) сокращается, следовательно, для оценки вектора коэффициентов знать её не нужно:

({{widehat{beta}}^{} = {({X’Omega^{- 1}X})}^{- 1}}X^{‘}Omega^{- 1}{y =}left( {X’begin{pmatrix} begin{matrix} z_{1}^{2} & 0 \ 0 & z_{2}^{2} \ end{matrix} & begin{matrix} ldots & 0 \ ldots & 0 \ end{matrix} \ begin{matrix} ldots & ldots \ 0 & 0 \ end{matrix} & begin{matrix} ldots & ldots \ ldots & z_{n}^{2} \ end{matrix} \ end{pmatrix}^{- 1}X} right)^{- 1}X’begin{pmatrix} begin{matrix} z_{1}^{2} & 0 \ 0 & z_{2}^{2} \ end{matrix} & begin{matrix} ldots & 0 \ ldots & 0 \ end{matrix} \ begin{matrix} ldots & ldots \ 0 & 0 \ end{matrix} & begin{matrix} ldots & ldots \ ldots & z_{n}^{2} \ end{matrix} \ end{pmatrix}^{- 1}y)

* * *

Ещё одна важная ситуация, когда с успехом может быть применен доступный ОМНК — это модель со случайными эффектами, которую мы рассмотрим в главе, посвященной панельным данным.

Источник

Обобщённый метод наименьших квадратов (ОМНК, GLS — англ. Generalized Least Squares) — метод оценки параметров регрессионных моделей, являющийся обобщением классического метода наименьших квадратов. Обобщённый метод наименьших квадратов сводится к минимизации «обобщённой суммы квадратов» остатков регрессии — $e^{T}We$ , где $e$ — вектор остатков, $W$ — симметрическая положительно определенная весовая матрица. Обычный МНК является частным случаем обобщённого, когда весовая матрица пропорциональна единичной.

Содержание

1 Сущность обобщённого МНК
2 Доступный ОМНК (FGLS, Feasible GLS)
3 Взвешенный МНК
- 3.1 Дисперсия ошибки пропорциональна квадрату некоторой переменной
- 3.2 Однородные группы наблюдений
4 ОМНК в случае автокорреляции
- 4.1 Процедура Кохрейна-Оркатта
- 4.2 Процедура Хилдрета — Лу
- 4.3 Процедура Дарбина
5 См. также
6 Литература

Сущность обобщённого МНК

Известно, что симметрическую положительно определенную матрицу можно разложить как $W=P^{T}P$ , где P- некоторая невырожденная квадратная матрица. Тогда обобщённая сумма квадратов может быть представлена как сумма квадратов преобразованных (с помощью P) остатков $(Pe)^{T}Pe$ . Для линейной регрессии $y=Xb+varepsilon$ это означает, что минимизируется величина:

$[P(y-Xb)]^{T}[P(y-Xb)]=(Py-PXb)^{T}(Py-PXb)=(y^{*}-X^{*}b)^{T}(y^{*}-X^{*}b)~,$

где $y^{*}=Py~,~X^{*}=PX$ , то есть фактически суть обобщённого МНК сводится к линейному преобразованию данных и применению к этим данным обычного МНК. Если в качестве весовой матрицы $W$ используется обратная ковариационная матрица $V$ случайных ошибок $varepsilon$ (то есть $W=V^{{-1}}$ ), преобразование P приводит к тому, что преобразованная модель удовлетворяет классическим предположениям (Гаусса-Маркова), следовательно оценки параметров с помощью обычного МНК будут наиболее эффективными в классе линейных несмещенных оценок. А поскольку параметры исходной и преобразованной модели одинаковы, то отсюда следует утверждение — оценки ОМНК являются наиболее эффективными в классе линейных несмещенных оценок (теорема Айткена). Формула обобщённого МНК имеет вид:

${hat {b}}_{{GLS}}=(X^{T}V^{{-1}}X)^{{-1}}X^{T}V^{{-1}}y$

Ковариационная матрица этих оценок равна:

$V({hat {b}}_{{GLS}})=(X^{T}V^{{-1}}X)^{{-1}}$

Доступный ОМНК (FGLS, Feasible GLS)

Проблема применения обобщённого МНК заключается в неизвестности ковариационной матрицы случайных ошибок. Поэтому на практике используют доступный вариант ОМНК, когда вместо V используется её некоторая оценка. Однако, и в этом случае возникает проблема: количество независимых элементов коварационной матрицы равно $n(n+1)/2$ , где $n$ -количество наблюдений (для примера — при 100 наблюдениях нужно оценить 5050 параметров!). Следовательно, такой вариант не позволит получить качественные оценки параметров. На практике делаются дополнительные предположения о структуре ковариационной матрицы, то есть предполагается, что элементы ковариационной матрицы зависят от небольшого числа неизвестных параметров $theta$ . Их количество должно быть намного меньше числа наблюдений. Сначала применяется обычный МНК, получают остатки, затем на их основе оцениваются указанные параметры $theta$ . С помощью полученных оценок оценивают ковариационную матрицу ошибок и применяют обобщённый МНК с этой матрицей. В этом суть доступного ОМНК. Доказано, что при некоторых достаточно общих условиях, если оценки $theta$ состоятельны, то и оценки доступного ОМНК будут состоятельны.

Взвешенный МНК

Дисперсия ошибки пропорциональна квадрату некоторой переменной

Однородные группы наблюдений

Пусть имеется n наблюдений разбитых на m однородных групп, внутри каждой из которых предполагается одинаковая дисперсия. В этом случае сначала модель оценивают обычным МНК и находят остатки. По остаткам внутри каждой группы оценивают дисперсии $sigma _{j}^{2}~,~j=1..m$ ошибок групп как отношение сумм квадратов остатков к количеству наблюдений в группе. Далее данные каждой j-й группы наблюдений делятся на $sigma _{j}$ и к преобразованным подобным образом данным применяется обычный МНК для оценки параметров.

ОМНК в случае автокорреляции

Если случайные ошибки подчиняются AR(1) модели $varepsilon _{t}=rvarepsilon _{{t-1}}+u_{t}$ , то без учета первого наблюдения преобразование P будет заключаться в следующем: из текущего значения переменных отнимаются предыдущие, умноженные на $r$ :

${begin{cases}y_{t}^{*}=y_{t}-ry_{{t-1}}\x_{t}^{*}=x_{t}-rx_{{t-1}}\b_{i}^{*}=b_{i},i>0\b_{0}^{*}=b_{0}(1-r)end{cases}}$

Данное преобразование называется авторегрессионным преобразованием. Для первого наблюдения применяется поправка Прайса — Уинстена — данные первого наблюдения умножаются на ${sqrt {1-r^{2}}}$ . Случайная ошибка преобразованной модели равна $u_{t}$ , которая по предположению есть белый шум. Следовательно применение обычного МНК позволит получить качественные оценки такой модели.

Поскольку коэффициент авторегрессии неизвестен, то применяются различные процедуры доступного ОМНК.

Процедура Кохрейна-Оркатта

Шаг 1. Оценка исходной модели методом наименьших квадратов и получение остатков модели.

Процедура Хилдрета — Лу

Процедура Дарбина

Преобразованная модель имеет вид:

$y_{t}-ry_{{t-1}}=b_{0}(1-r)+sum _{{i=1}}^{k}b_{j}(x_{{tj}}-rx_{{t-1j}})+varepsilon _{t}-rvarepsilon _{{t-1}}$

Раскрыв скобки и перенеся лаговую зависимую переменную вправо получаем

$y_{t}=b_{0}(1-r)+ry_{{t-1}}+sum _{{j=1}}^{k}b_{j}x_{{tj}}-sum _{{j=1}}^{k}b_{j}rx_{{t-1j}}+varepsilon _{t}-rvarepsilon _{{t-1}}$

Введем обозначения $b_{0}(1-r)=a_{0},~-rb_{j}=a_{j},~u_{t}=varepsilon _{t}-rvarepsilon _{{t-1}}$ . Тогда имеем следующую модель

$y_{t}=a_{0}+ry_{{t-1}}+sum _{{j=1}}^{k}b_{j}x_{{tj}}+sum _{{j=1}}^{k}a_{j}x_{{t-1j}}+u_{t}$

Данную модель необходимо оценить с помощью обычного МНК. Тогда коэффициенты исходной модели восстанавливаются как ${hat {b}}_{0}={hat {a}}_{0}/(1-{hat {r}}),~{hat {b}}_{j}=-{hat {a}}_{j}/{hat {r}}$ .

При этом полученная оценка коэффициента автокорреляции может быть использована для авторегрессионного преобразования и применения МНК для этой преобразованной модели для получения более точных оценок параметров.

См. также

Метод наименьших квадратов

Литература

Магнус Я.Р. Катышев П.К. Пересецкий А.А. Эконометрика. Начальный курс . — 2004.

Источник

Целесообразно использовать обобщенный метод наименьших квадратов если ошибки модели

Обобщенный метод наименьших квадратов (омнк)

Сущность обобщённого МНК

Доступный ОМНК (FGLS, Feasible GLS)

Взвешенный МНК

Дисперсия ошибки пропорциональна квадрату некоторой переменной

Однородные группы наблюдений

ОМНК в случае автокорреляции

Процедура Кохрейна-Оркатта

Процедура Хилдрета — Лу

Процедура Дарбина

См. также

Литература

Содержание

Сущность обобщённого МНК

Доступный ОМНК (FGLS, Feasible GLS)

Взвешенный МНК

Дисперсия ошибки пропорциональна квадрату некоторой переменной

Однородные группы наблюдений

ОМНК в случае автокорреляции

Процедура Кохрейна-Оркатта

Процедура Хилдрета — Лу

Процедура Дарбина

См. также

Литература

А вот еще интересные материалы: