View Original
X
Эллипсы и прямоугольники ошибок
Программные продукты и их версии
AutoCAD Civil 3D 2017
Автор: 
Help
После корректировки по методу наименьших квадратов ковариационная матрица используется для вычисления среднеквадратических отклонений положения ![]() и
и ![]() .
.
На следующем рисунке показаны среднеквадратические отклонения, представляющие полуразмеры среднеквадратической 68% вероятности прямоугольника ошибок вокруг каждой точки:
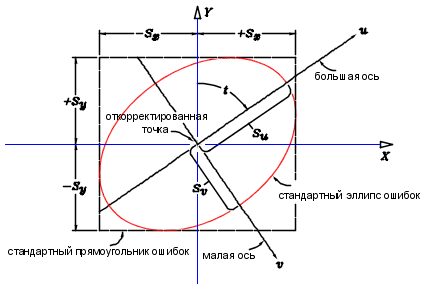
Где:
- t = ориентация эллипса ошибок, направления большой полуоси
- u = большая полуось эллипса ошибок
- v = малая полуось эллипса ошибок
- x = половина ширины прямоугольника ошибок
- у = половина высоты прямоугольника ошибок
- S = среднеквадратическое отклонения положения точки
Графическое представление результатов измерений
В ряде случаев при обработке результатов
измерений пользуются графическим
методом. Графическое представление
результатов позволяет быстро понять
главные особенности наблюдаемой
зависимости и обнаружить ошибки в
измерениях.
Приведем
основные правила построения графиков.
-
Необходимо пользоваться листом
миллиметровой бумаги, размер которого
не должен превышать размер тетрадного
листа.

НеверноВерно
Рис.1.
Выбор масштаба и начала отсчета при
построении графиков
-
Важно разумно выбирать масштабы, чтобы
измеренные точки
располагались на всей площади листа.
На рис.1 изображены примеры неправильного
и правильного построения графиков.
На
левом (неправильно построенном) графике
экспериментальные точки занимают правую
нижнюю часть листа. Чтобы этого избежать,
следует выбрать более крупный масштаб
по оси Н
и сместить нуль на оси абсцисс, как это
сделано на правом графике.
Масштаб
должен быть удобным. Клеточка миллиметровой
бумаги должна соответствовать 0,1; 0,2;
0,5; 1; 2; 5; 10 и т.д. единицам измеряемой
величины, но не 3; 4; 7 и т.д.
-
Следует
стремиться к такому выбору величин,
откладываемых по осям, чтобы ожидаемая
зависимость имела вид прямой линии.
Так, исследуя закон падения тел, мы
вправе ожидать, что результаты будут
описываться законом
 .
.
Если откладывать по осям и
и или
или и
и ,
,
или и
и ,
,
то график приобретает вид прямой линии.
Одно из этих трех представлений и должно
быть выбрано при построении графика. -
Выполняя
измерения, необходимо стремиться к
тому, чтобы точки будущего графика
располагались достаточно равномерно.
Этого можно добиться следующим образом:
-
первые
два измерения провести при таких
параметрах установок, при которых точки
на графике будут максимально и минимально
удалены от начала координат (например,
измерить время падения тела с максимальной
и минимальной высот, реализуемых в
данной установке); -
с
учетом полученных результатов выбрать
удобный масштаб и нанести эти точки на
график; -
соединить
точки пунктирной линией и найти такие
параметры установки, при которых точки
на графике будут располагаться равномерно
(ориентировочное число точек указано
в описаниях лабораторных работ); -
провести
измерения при этих параметрах, результаты
занести в таблицу и построить график.
Мы
изложили самый простой способ графической
обработки результатов измерений.
В
табл.4 представлена зависимость времени
падения t
тела от высоты Н,
а также погрешности измерения этих
величин
![]() и
и![]()
Таблица 4
Экспериментальные данные и параметры, необходимые для построения графика
|
Номер строки |
Параметры |
Значения |
|||
|
1 |
Н, |
0,50 |
1,00 |
1,50 |
2,0 |
|
2 |
ΔН, |
0,04 |
0,06 |
0,10 |
0,10 |
|
3 |
t, |
0,32 |
0,48 |
0,55 |
0,64 |
|
4 |
Δt, |
0,02 |
0,02 |
0,03 |
0,03 |
|
5 |
t2, |
0,102 |
0,23 |
0,30 |
0,41 |
|
6 |
Δ(t2), |
0,013 |
0,02 |
0,03 |
0,04 |
Высота и время
падения связаны соотношением
![]()
поэтому
график удобно представить в координатах
![]() и
и![]() так
так
как в этих координатах зависимость
будет линейной. Поэтому в 5-й строке
табл.4 представлены значения![]() .
.
При
нанесении экспериментальных точек на
график необходимо указать погрешности.
Для расчета погрешности
![]() воспользуемся
воспользуемся
формулой (1) и получим:
![]() .
.
С
помощью этого выражения рассчитаем
соответствующие погрешности и занесем
их в 6-ю строку табл.4.
Построим
график. Для этого, выбрав масштаб вдоль
координатных осей (рис.2), нанесем
экспериментальные точки и погрешности.

Рис.2.
Пример построения графика
Погрешность
![]() откладывается по горизонтали вправо и
откладывается по горизонтали вправо и
влево от точки, а погрешность![]() — по вертикали вверх и вниз. В результате
— по вертикали вверх и вниз. В результате
получаются ″поля ошибок″ (прямоугольники
на графике). Сплошной линией представлена
изучаемая зависимость. Тот факт, что
она проходит через все ″поля ошибок″,
подтверждает, что![]() .
.
При графической обработке результатов
измерений часто определяют угловой
коэффициент
![]() прямой, который для нашего примера равен
прямой, который для нашего примера равен
![]() .
.
(3)
Определив из графика
![]() ,
,
по формуле (3) можно найти ускорение
свободного падения. Для нахождения
углового коэффициента необходимо
выполнить следующие операции:
-
провести пунктирные
прямые, имеющие максимальный и минимальный
наклоны и проходящие через все ″поля
ошибок″, и рассчитать максимальное
 и
и
минимальное значения углового коэффициента:
значения углового коэффициента:
![]()
![]()
-
вычислить
среднее значение и абсолютное значение
их полуразности:
![]()
![]()
Из
(3) и (1) следует
![]() ,
,![]()
Соседние файлы в папке Лабы
- #
- #
- #
- #
- #
- #
Дипломные работы, курсовые, контрольные, рефераты на заказ
Методические рекомендации особенности физических наблюдений.(4 часа)
Подобный материал:
- Методические рекомендации по проведению Единого Всекубанского классного часа, 33.75kb.
- Методические рекомендации «Педагогические особенности использования мультимедиа в образовании», 698.02kb.
- Постановлением Президиума Ростовского областного суда 6 августа 2004 года методические, 89.43kb.
- Методические рекомендации для учителей предметников по использованию цор в своей педагогической, 1201.3kb.
- Методические рекомендации по подготовке проекта муниципального правового акта органа, 154.99kb.
- Методические рекомендации и учебные материалы для проведения единого классного часа, 148.78kb.
- Методика преподавания темы «Многочлены» в профильной школе Методические рекомендации, 72.18kb.
- Основы метрологии в физике, 146.66kb.
- С. И. Сай «17» февраля 2003 года методические рекомендации, 234.96kb.
- Академия оценки и строительства казахстанская республиканская палата оценщиков особенности, 1159.14kb.
6/10. Определение погрешности измерений. Прямоугольник ошибок.
Дать понятие о погрешности измерений, ее влияние на вывод эмпирических зависимостей. Виды погрешностей. Погрешность измерительного прибора. Абсолютная погрешность. Погрешность отсчета. Прямоугольник ошибок.
Демонстрации
- Измерение объема колбы мензурками с разной ценой деления.
- Измерение длины нескольких тетрадных листов одной линейкой и определение среднего значения длины тетрадного листа.
— 8 —
- Определение толщины нити с помощью линейки с миллиметровыми делениями.
- Измерение длины парты линейкой, длина которой не превышает 30 см.
- Определение погрешности скорости равномерного движения математическими методами.
- Погрешность, вызываемая округлением величин.
- Построить график зависимости силы тяжести от массы, определить цену деления динамометра, точность измерения массы и указать на графике прямоугольник ошибок.
Лабораторные работы и опыты
- При измерении длины с помощью ученической линейки может быть допущена ошибка за счет неправильного расположения глаза. Как измерять правильно? Чем вызывается ошибка при таких измерениях?
- Дана таблица измерений приложенной нагрузки от положения конца образца. Постройте график этой зависимости и проанализируйте погрешности измерений на разных его участках.
| 0 | 100 | 200 | 300 | 400 | 500 | 600 | 700 | 800 | 900 | 1000 | 1100 | Нагрузка |
| 0 | 2,1 | 4,2 | 6,3 | 8,5 | 10,6 | 12,6 | 14,6 | 16,6 | 18,6 | 20,5 | 22,3 | Растяжение |
Самостоятельные работы
- Рассмотрите шприц и охарактеризуйте его как измерительный прибор.. Определите погрешность, верхний и нижний пределы его измерений.
- Определите с земли высоту дерева, телеграфного столба или любого другого предмета, имея только небольшую линейку. Предложите несколько способов. Оцените погрешность каждого способа.
- Измерить площадь фигуры неправильной формы и подсчитать погрешность своих измерений.
7/11. Измерение коэффициента упругости пружин различной жесткости с помощью графика.
Графическая зависимость силы упругости от растяжения. Расчет коэффициента упругости с помощью графика.
Демонстрации Измерение растяжения пружин разной жесткости под действием различных сил.
Лабораторные работы и опыты
Измерение коэффициента упругости пружин различной жесткости с помощью графика.

Самостоятельные работы
Начертить график зависимости силы упругости от деформации на миллиметровой бумаге, подсчитать погрешность опыта, построить прямоугольник ошибок и вычислить коэффициент упругости пружины.
8/12. Сила трения. Измерение коэффициента трения.
Сила трения покоя, скольжения, качения. Зависимость силы трения от силы нормального давления. Коэффициент трения. Шероховатости соприкасающихся поверхностей, взаимодействие молекул. Жидкое трение.
Демонстрации
— 9 —
- Трение скольжения, покоя и качения. Равновесие тела на вращающемся диске.
- Смазывание трущихся поверхностей уменьшает трение. Почему же труднее удерживать рукоятку топора сухой рукой, чем влажной?
Лабораторные работы и опыты
Изучение зависимости силы трения скольжения от силы давления. Результат получить аналитически и графически.
Самостоятельные работы
- Карандаш удерживают на столе в вертикальном положении заостренным концом вниз. После того как его отпустили, он начинает падать, как движется при этом острие карандаша в зависимости от коэффициента трения? Оторвется ли острие карандаша от стола (в отличие от случая, когда в результате скольжения место заточки карандаша в конце концов соприкоснется со столом )?
- Карандаш находится в горизонтальном положении, опираясь концами на два моих указательных пальца. Пока я медленно сдвигаю пальцы, чтобы они встретились под центром стержня, он скользит либо по одному, либо по другому пальцу. Почему он так движется?
9/13. Закон инерции. Законы взаимодействия.
Фундаментальные законы взаимодействия. Их значение для становления физики как науки. Связь действующей силы с изменением скорости. Движение с постоянной скоростью.
Демонстрации
- Расположите на столе близко друг к другу два алюминиевых бруска. Свяжите ножки пинцета и поместите его между брусками. Пережгите нить. Почему бруски приходят в движение? Одинаковы ли их скорости? Массы?
- Повторите опыт, взяв бруски одинакового объема, но разных масс. Одинаковы ли их скорости?
- Демонстрация законов инерции.
Приборы и материалы. Бумажная тарелка, ножницы, бумажный шарик.
Ход работы.
- Отрежьте от тарелки одну половину.
- Поместите шарик на кромку отрезанной части.
- Поставьте тарелку на стол и слегка наклоните ее, чтобы шарик быстро покатился по выемке тарелки.
Шарик скатывается с тарелки и удаляется от нее по прямой.
Вывод. Предметы движутся по прямой, если на них не действуют никакие силы.
- Положите лист картона так, чтобы он опирался на две книги. На середину листа положите мешочек с песком. Резко поднимите лист вместе с мешочком. Почему изменилась его форма?
— 10 —
- Действие равно противодействию. Но почему тело движется, ведь какую бы силу мы не приложили, появится противодействующая сила. Где здесь ошибка в рассуждениях?
Лабораторные работы и опыты
- Положите шарик на лист бумаги. Отметьте положение шарика относительно стола. Выдерните лист резким движением. Изменилось ли положение шарика?
- Подвесите алюминиевый и медный цилиндры на нить к лапке штатива. Отклоните их в разные стороны и проследите, что с ними происходит после удара.
- Зацепите крючками два динамометра и слегка разведите их в стороны. Заметьте их показания.
Самостоятельные работы
- Придумайте и проделайте опыты, при помощи которых можно показать проявление инерции у покоящихся и движущихся тел.
- Придумайте опыты, при помощи которых можно показать зависимость инертности тел от массы.
- Висящий на нити, привязанной к потолку каюты, груз отклонился в сторону, хотя на него ничто не действовало. Нет ли здесь противоречия с законом инерции?
- Свойством инерции обладают не только твердые, но также жидкие и газообразные тела. Придумайте и проделайте опыты, при помощи которых можно показать проявление инерции жидких тел.
- Предмет покоится на краю горизонтального стола. Его толкают и он падает с другой стороны стола, ширина которого 1 м, через 2 с. Есть ли у предмета колеса?
10/14. Скорость равномерного движения. Относительность движения.
Мгновенная скорость. Скорость равномерного движения. Относительность движения. Относительная скорость тел. Расчет скорости движения для равномерного движения. Средняя скорость.
Демонстрации
- Самолет, летящий со скоростью 900 км/ч, во время полета заправляется горючим от другого самолета. С какой скоростью движется при этом самолет-заправщик?
- Демонстрация относительности движения на примере тележки и вращающегося диска, установленного на штативе.
- Демонстрация теневой проекции вращения тела, лежащего на горизонтально расположенном диске.
- Автомобиль проехал 60 км за 1 ч, а потом еще 240 км за 5 ч. Какова средняя скорость на всем пути?
- Двигаясь по шоссе, велосипедист проехал 900 м со скоростью 15 м/с, а затем по плохой дороге 400 м со скоростью 10 м/с. С какой средней скоростью он проехал весь путь?
- Минутная стрелка настенных часов вдвое длиннее, чем часовая. В какой момент после полуночи конец минутной стрелки будет удаляться от конца часовой стрелки с наибольшей скоростью?
Лабораторные работы и опыты
- Положите линейку на лист бумаги. Один конец линейки зажмите и с помощью карандаша переместите на некоторый угол. Определите траекторию, скорость и перемещение относительно линейки и листа бумаги.
- Положите деревянный брусок на лист бумаги. Медленно потяните за край листа. В каком состоянии относительно стола находится лист бумаги и брусок? В каком состоянии относительно листа бумаги находился брусок?
— 11 —
- Положите брусок на лист бумаги и резко потяните за край листа. В каком состоянии относительно стола находился лист бумаги? В каком состоянии относительно бумаги находился стол? В каком состоянии относительно стола находился брусок?
- Можно ли сказать, что брусок движется относительно стола в опытах, указанных в предыдущих задачах?
Самостоятельные работы
- Подсчитайте скорость своего подъема по лестнице.
- Определите среднюю скорость движения автобуса между остановками и переведите ее в м/с.
- Определите скорость, с которой перемещается конец минутной стрелки ваших часов.
- Голодный паук приготовился поймать насекомое, если оно окажется в паутинке, которая натянута между ним и стеной. Длина нити 1 м. на нить попала гусеница. Увидев паука, она стала уползать от него к стене со скоростью ν1= 1мм/с относительно нити, а паук , оставаясь на месте, стал вытягивать свой конец нити со скоростью ν0= 1 см/с, считая, что нить может растягиваться без ограничений. Доползет ли гусеница до стены? Как изменится решение предыдущей задачи, если паук не сидит на месте, а удаляется от стены, увлекая за собой конец нити?
11/15. Перемещение при равномерном движении.
Траектория. Перемещение. Путь. Связь пути и перемещения при прямолинейном равномерном движении.
Демонстрации
Сравнить движение стрелок часов; нитяного маятника; равномерное движение тележки, привязанной к грузу, подвешенному к ней через блок. На тележке стоит капельница, с помощью которой отмечаются величины перемещений за равные промежутки времени. Вращение диска с закрепленной осью.
Лабораторные работы и опыты
Расположите резиновую трубку, заполненную водой, вертикально. Перевернув трубку, проследите за движением пузырька воздуха в ней. Отмерив одинаковые расстояния, проследите за тем, соответствуют ли ударам метронома прохождение пузырьком сделанных вами меток.
Самостоятельные работы
- Определите путь и перемещение минутной стрелки часов за 10 минут, 30 минут и 1 час.
- В движущемся вагоне в любой момент времени есть точки, движущиеся в сторону, обратную движению вагона. Какие это точки?
- Две одинаковые шайбы А и В скользят без трения по льду озера. Они соединены легкой, нерастяжимой, но упругой нитью длиной √2L. В момент времени t = 0 шайба А покоится в точке с координатами (0,0), а шайба В, которая находится в точке с координатами (L,0), сообщают скорость v вдоль оси y в положительном направлении. Определите координаты и скорости шайб А и В в моменты времени t1 = 2L/v и t2 = 100L /v.
12/16. Графики зависимости скорости и перемещения от времени.
Научить строить и читать графики равномерного движения.
1. Получены данные о движения автомобиля:
| Длительность движения,ч | 0,1 | 0,4 | 0,2 |
| Скорость, км/ч | 20 | 60 | 20 |
— 12 —
- Какой путь пройдет автомобиль за первый промежуток времени?
- Какова общая длина пути, пройденного автомобилем?
- Постройте график зависимости скорости от времени для этой поездки
- За какое время автомобиль пройдет первые 14 км пути?
- Укажите площадь на вашем графике, соответствующую первым 14 км пути.
2. Проанализируем графики, приведенные ниже. Какие из них могут соответствовать графикам зависимости перемещения от времени и почему? Какие из них могут соответствовать графикам зависимости скорости равномерного движения от времени и почему?
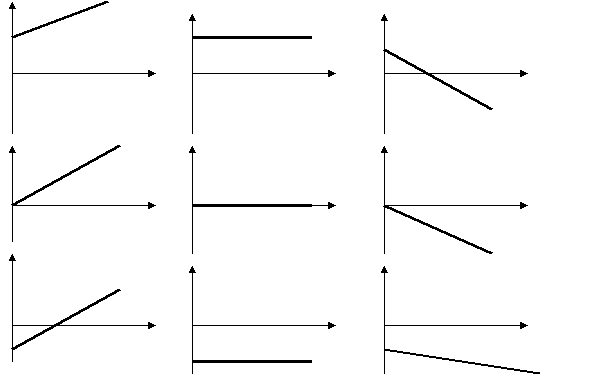
Лабораторные работы и опыты
Проследим, как движутся пузырьки воздуха со дна водоема. Проанализируем фотографии, сделанные за одинаковые промежутки времени. Измеряя перемещения пузырьков, запишем результаты в таблицу.
| x, cм | ||||
| t, c |
По полученным данным построим график зависимости перемещения от времени.
Самостоятельные работы
На рисунке представлены графики проекций скоростей двух автомобилей, движущихся по одной прямой. Что можно сказать о направлении движения автомобилей? Меняются ли их скорости со временем? Какой из автомобилей движется быстрее?
— 13 —
13/17. Координатный метод описания движения.
Движение-это изменение положения тела относительно данного тела отсчета и связанной с ним системы координат с течением времени. Система отсчета и система координат. Положение тела в одномерной, двумерной и трехмерной системе координат. Угловая система координат.
Демонстрации
- Все вы знаете стихотворение А. С. Пушкина «У лукоморья дуб зеленый…». Что является телом отсчета для описания движения кота?
- Определим координаты люстры в классе, выбрав за тело отсчета входную дверь.
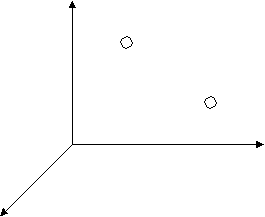
- На рисунке изображено положение двух точек в пространстве относительно координатных осей. Определить:
Цену деления осей
Координаты точки А.
Координаты точки В.
Лабораторные работы и опыты
На рисунке показано положение трех точек А, В и С, соединенных между собой кривой линией. Эта линия является траекторией движения точки из А в С. Определить:
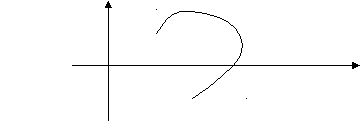 x
x
- Цену деления осей координат
- Координаты точек А, В и С.
- Проекции вектора АВ, ВС и АС.
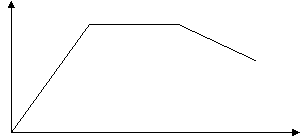
На рисунке изображен график координаты тела от времени. Определите:
- Цену деления осей.
- Время движения по оси ох
- Время остановки
- Время движения против оси ох
- Пройденный путь
- Среднюю скорость движения
- Скорость до остановки
- Скорость после остановки
- Величину перемещения
— 14 —
X,м
 t,c
t,c
Самостоятельные работы
С помощью рулетки или сантиметровой измерительной ленты определите координаты точки подвеса комнатного светильника по отношению к системе отсчета, связанной с одним из нижних углов комнаты. Координаты оси направьте вдоль стен комнаты.
14/18. Движение с ускорением.
Движение с изменяющейся во времени скоростью. Ускорение. Перемещение при прямолинейном равноускоренном движении. Изменение скорости по направлению при вращении стрелок часов.
Демонстрации
1. Видеофильм «Основы кинематики». Элемент технологии критического мышления И.Д.Е.А.Л.
- Формулировка проблемы (все ли тела движутся равномерно)
- Формулировка проблемы в виде вопроса (как можно описать движение тел, отличающихся от равномерного)
- Генерирование как можно большего числа решений вопроса
- Выбор наилучших вариантов
- Характер изменения физические величины при движении со скоростью, меняющейся во времени
Оформление решения проблемы
2. Конический маятник.
3. Проделайте опыт Г.Галилея: убедитесь в том, что пути, проходимые в последовательные равные промежутки времени, относятся как последовательный ряд нечетных чисел. Положив шарик вверху желоба, отпустите его и карандашом отметьте местоположения шарика под удары метронома. Пути, проходимые при равноускоренном движении за последовательные равные промежутки времени, определите по миллиметровой шкале на линейке. Наклонная плоскость должна составлять малый угол с плоскостью стола, для того чтобы шарик скатывался медленно.
Лабораторные работы и опыты
Определите среднюю скорость шарика, скатывающегося с наклонной плоскости. Как она зависит от угла наклона плоскости? От чего зависит точность ваших измерений? Как определить конечную скорость шарика? Как она зависит от угла наклонной плоскости и ее длины?
Самостоятельные работы
Пластиковый пузырек с подкрашенной жидкостью поставить на тележку и открыть отверстие в дне сосуда. Измерить расстояния между каплями, оставленными на бумажной ленте, положенной на демонстрационный стол, при скатывании тележки с наклонной плоскости, а также общее время движения и интервалы времени, соответствующие отметкам на ленте. Подсчитать среднюю скорость движения.
— 15 —
15/19. Свободное падение тел.
Движение тела из состояния покоя под действием силы тяжести. Постоянство ускорения свободного падения для данного места на земной поверхности. Измерение ускорения свободного падения.
Демонстрации
- Определите экспериментально ускорение, с которым шарик скатывается по наклонному желобу. Как изменяется ускорение шарика при увеличении угла наклона желоба?
- Шарик упал со стола. С каким ускорением он двигался? Сколько времени длилось падение шарика? Какой была скорость шарика в момент, когда он коснулся пола? Какова высота стола?
Лабораторные работы и опыты
- Пронаблюдайте за падением тел разной массы, но одинакового объема; разной формы. Сделайте вывод.
- Придумать опыт, доказывающий, что свободно падающий шарик движется по вертикали.
Самостоятельные работы
- Определите ускорение свободного падения, пользуясь отвесом, секундомером и камнями различной формы и объема. Местом проведения опыта может быть высокий мост, глубокий овраг или балкон многоэтажного дома. Возьмите округленный камень небольших размеров и под счет “раз, два, пуск” предоставьте ему возможность падать. Секундомером измерьте время падения камня, а затем по известной формуле найдите ускорение свободного падения. Повторите опыт несколько раз с разными телами и убедитесь в том, что ускорение свободного падения не зависит от массы падающего тела. Как влияет на результат расчета ускорения свободного падения погрешность измерения времени и время реакции человека?
- Маленький шарик В лежит на краю стола высотой 1 м, другой такой же шарик А подвешен на нити длинной 1 м и представляет собой математический маятник. Если нить с шариком А привести в горизонтальное положение и отпустить, то между шариками произойдет упругое столкновение. Рассматривая движение шарика В только до момента его падения на землю, ответьте на вопросы: а) какой шарик дольше находится в движении; б) у какого шарика больше длина траектории?
16/20. График скорости от времени при равноускоренном движении.
График скорости от времени при равномерном движении (повторение). Отличие графика скорости неравномерного движения от графика скорости для равномерного движения. Физический смысл угла наклона графика. График скорости свободно падающего тела. Угол наклона графика скорости тела, движущегося под действием силы тяжести.
Основной материал
- В таблице приведены значения мгновенной скорости автомобиля от времени:
| Время,с | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
| Скорость, м/с | 10,0 | 12,4 | 14,8 | 17,2 | 19,6 | 22,0 | 24,4 |
Постройте график скорости от времени для этой поездки и ответьте на вопросы:
- С какой скоростью двигался автомобиль в моменты времени 2,6 с и 4,8 с?
- Какой путь прошел автомобиль между этими двумя моментами времени?
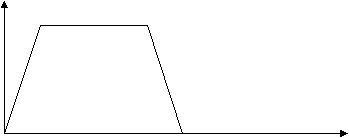
2. Дан график скорости от времени.
— 16 —
V,м/c
 t,c
t,c
Разобрать, как меняется скорость движения велосипедиста по графику. Какое время он двигался равномерно? Какое расстояние он проехал, двигаясь с постоянной скоростью, при разгоне и при торможении?
Лабораторные работы и опыты
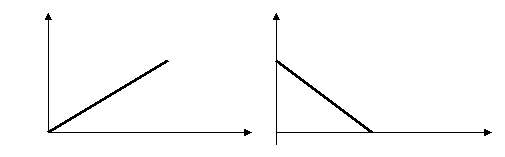
По графику скорости найдите ускорение и среднюю скорость за первые две секунды его
движения.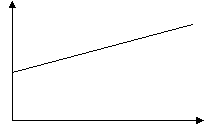 t,c
t,c
Самостоятельные работы
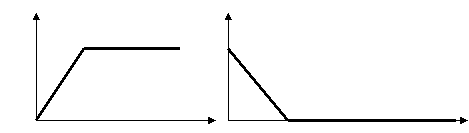 t,c
t,c
 t,c
t,c
Определите ускорение и среднюю скорость тел, пользуясь графиками скорости от времени.
Давайте знакомиться: я Меликян Маргарита, кандидат физико-математических наук, уже 4й год работаю на мехмате МГУ и кафедре высшей математики МФТИ, а также несколько лет как преподаю в ШАД Helper. Преподаю я как разнообразные курсы из блока анализа, так и вероятностного блока, и сегодня я хочу немного поговорить о том, каково это – осваивать математический анализ и каких ошибок следует избегать, какие лайфхаки применить.
Первая препона, с которой сталкивается человек в самом начале освоения новой дисциплины, даже если он это делает “под присмотром” преподавателя – это литература. На что нужно обращать внимание и ориентироваться при выборе?
-
В первую очередь на то, какую литературу предлагает сам преподаватель. Если он ее предлагает, то скорее всего его подход в изложении материала будет близок тому, что вы увидите в соответствующих книжках, однако на самом деле списки литературы часто бывают шире и разнообразнее, и отсюда произрастает необходимость второго пункта ⇒
-
Я очень не советую новичкам пользоваться большим количеством литературы одновременно! Во-первых, от обилия информации и осознания количества того, что надо освоить, ваш запал может иссякнуть гораздо раньше, чем вы хоть сколько-нибудь продвинетесь в изучении. Во-вторых, что страшнее, вы можете попасть в неприятные “циклы”:
В книге А: доказали теорему 1, из нее следует теорема 2.
В книге Б: доказали теорему 2, а из нее теорему 1.А теперь задумайтесь, что получается, если вы решили взять, скажем, доказательство теоремы 1 из книжки Б, а доказательство теоремы 2 из книжки А… Впрочем, если вы решили, что вам не сильно-то интересны и нужны доказательства и строгое пирамидное развитие теории, то это может быть не так уж страшно, кроме того, что породит у вас искаженное представление о “действительности”. Тут же замечу, что полностью игнорировать изучение доказательств так себе идея ввиду того, что некоторые из них используют приёмы и идеи, полезные для решения задач. А нас же в конечном итоге интересует совершенствование в этом плане, да?)
-
Конечно же, учитывая всё вышесказанное, выбирать стоит из предложенного того автора, чье изложение материала показалось вам ближе всего (т.е. понятнее и доступнее). Для определения фаворита можно почитать одну и ту же тему в разных учебниках и прислушаться к себе 😉
-
И специально для студентов ВУЗов: С БОЛЬШОЙ ОСТОРОЖНОСТЬЮ ПОЛЬЗУЙТЕСЬ “МЕТОДИЧКАМИ” от старшекурсников. Обязательно сверяйтесь с учебниками касательно написанного. Потому как это тот тип литературы, который просто кишит неточностями, ошибками и совсем уж невероятными фактами. Их можно читать только уже разобравшись в предмете, как научпоп или фантастику.
Впрочем, всё изложенное выше можно отнести не только к математическому анализу, но и к любой другой математической дисциплине (а может, и не только математической, вот за это не ручаюсь).
Второй момент, который оказывается на первом курсе затруднительным, это гениальный аппарат – “эпсилон-дельта определения” и иже с ними. Определения, заключающие в себе набор символов, среди которых понакиданы кванторы (порой до 3х разных типов в одной математической “фразе”!) вперемежку с множествами/пространствами, их элементами и еще бог знает чем вызывают нереальные трудности при запоминании! Что очень часто демонстрируют студенты на коллоквиумах, зачётах, экзаменах…
Кто виноват?
И что делать?
Ответ прост и сложен одновременно – не механически “заучивать” (я искренне считаю, что просто запомнить такой объём информации нереально, да и излишне), а попробовать ПОНЯТЬ, “что хотел сказать автор”. Понять, почему темы изучаются именно в таком порядке, обычно это обусловлено некоторой логикой усложнения понятий. Собственно, за что обожаю математику: объём информации, требуемой к запоминанию, выгодно отличается от гуманитарных направлений 🙂 Если вы понимаете, “чувствуете”, что там происходит, можете сами написать на математическом языке нужное определение или вывести нужное утверждение, вам становится гораздо, нет, не так, ГОРАЗДО легче!
Хорошо, тезис, думаю, ясен, а как понять-то? Приведу парочку лайфхаков:
-
Раз уж мы начали с “эпсилон-дельта определений” и аналогичного, то давайте про них и поговорим. Первое, что вам может помочь – попробуйте попереставлять кванторы всевозможными способами или заменить их на другие, “забыть” вовсе (одним словом, смоделировать реальный ответ недоучившего на экзамене), и посмотреть, что из этого получится. Возможно ли подобрать такой объект? а если возможно, то будет ли это то, чего нам хотелось изначально?
Например, вы пытаетесь разобраться с критерием Коши сходимости последовательности. Один из вариантов написания условия Коши фундаментальности последовательности
выглядит так:
Что будет, если мы переставим один из кванторов в начало? То есть
Даст ли нам это сходящуюся последовательность? Или нет?
-
Второй лайфхак удаётся применить не везде, но тоже довольно важен – это попытка понять, а есть ли геометрическая или физическая интерпретация того или иного понятия/свойства? Эти интерпретации также порой помогают понять, возможно ли то, про что спрашивают в задаче, что вероятнее: обладает функция тем или иным свойством или нет?
Например, производная одномерной функции (можно считать, что от времени) – это мгновенная скорость траектории точки в данный момент времени. Может ли точка начать движение с положительной скоростью, двигаться гладко, сменить скорость на отрицательную, обойдя стороной момент остановки?
А что для функции означает то, что она непрерывна? А равномерно непрерывна? -
Большое количество утверждений с самыми разными требованиями к объектам в них тоже могут вызывать затруднения. Как помочь себе запомнить, что где требовать? Да и вообще, какие из условий являются техническими (т.е. без них доказательство становится в разы сложнее), а какие по существу (то есть выкину и всё, найдётся контрпример)? Хороший способ – попробовать повыкидывать условия и попридумывать контрпримеры.
Пример. Рассматриваете теорему об обратной функции. Самый простой вариант: вам дают функцию на отрезке и требуют там её непрерывности и строгой монотонности. Что будет, если убрать одно из условий? Всегда ли получится ввести обратную функцию? А бывают ли функции, не удовлетворяющие одному из условий, но тем не менее имеющие обратную?
-
Этот момент в целом можно было озвучить еще при обсуждении литературы, но мне захотелось его выделить особенно, так как на мой взгляд он архиважен. А именно:
при изучении утверждений обращайте внимание на принятые в соответствующем источнике определения объектов и обозначения. Под словом “гладкая” могут скрываться функции разной степени “хорошести”, или, например, у одного автора в утверждении дополнительно указано, что функция должна быть ограничена, у другого нет, кто прав? Да, возможно, оба, просто один понимает, скажем, интеграл Римана как предел интегральных сумм, и тогда ограниченность функции – необходимое условие интегрируемости, а другой ввёл его через суммы Дарбу, для чего ограниченность пришлось “вшить” в определение. И тогда в утверждении вновь подчеркивать ограниченность нет никакой нужды. Оба определения при этом приводят к рассмотрению одного и того же объекта в итоге, но чисто формально утверждения будут отличаться. Отличная ловушка для читателя!
На этом на сегодня всё, удачи вам в познании!
P.S. И не расстраивайтесь, если при применении некоторых лайфхаков поставите себе задачи, на которые не получается дать ответы, да и даже загуглить не удаётся – это нормально, порой задачам надо дать время осесть… или же обсудить с товарищами по несчастью 🙂 Или же просто отпустить (ситуацию)).
P.P.S. Ответы на вопросы в тексте:
-
Критерий Коши. Нет, не даст. Рассмотрите последовательность
или
.
-
Про точку: нет, не может (теорема о нулях функции).
Непрерывность в точке: при рассмотрении графика исследуемой функции получается, что сколь малый эпсилон мы бы ни взяли (это будет половиной высоты прямоугольника без границы, который мы строим, отступив вверх и вниз от уровня, равного значению функции в рассматриваемой точке), для него всегда найдётся дельта (половина ширины прямоугольника), такое что, взяв произвольный аргумент со стороны прямоугольника, параллельной оси абсцисс, я обнаружу, что значение функции в этом аргументе попадает вовнутрь построенного прямоугольника. В равномерной непрерывности мы построение чуть видоизменяем: выбрать дельта можно так, что прямоугольник со сторонами дельта и эпсилон можно двигать по всему множеству, на котором функция претендует на равномерную непрерывность, и при этом функция не будет пересекать стороны прямоугольника, параллельные оси абсцисс. -
Не всегда, рассмотрите функцию
Существуют:
на отрезке [−1; 1].
Давайте знакомиться: я Меликян Маргарита, кандидат физико-математических наук, уже 4й год работаю на мехмате МГУ и кафедре высшей математики МФТИ, а также несколько лет как преподаю в ШАД Helper. Преподаю я как разнообразные курсы из блока анализа, так и вероятностного блока, и сегодня я хочу немного поговорить о том, каково это – осваивать математический анализ и каких ошибок следует избегать, какие лайфхаки применить.
Первая препона, с которой сталкивается человек в самом начале освоения новой дисциплины, даже если он это делает “под присмотром” преподавателя – это литература. На что нужно обращать внимание и ориентироваться при выборе?
-
В первую очередь на то, какую литературу предлагает сам преподаватель. Если он ее предлагает, то скорее всего его подход в изложении материала будет близок тому, что вы увидите в соответствующих книжках, однако на самом деле списки литературы часто бывают шире и разнообразнее, и отсюда произрастает необходимость второго пункта =⇒
-
Я очень не советую новичкам пользоваться большим количеством литературы одновременно! Во-первых, от обилия информации и осознания количества того, что надо освоить, ваш запал может иссякнуть гораздо раньше, чем вы хоть сколько-нибудь продвинетесь в изучении. Во-вторых, что страшнее, вы можете попасть в неприятные “циклы”:
В книге А: доказали теорему 1, из нее следует теорема 2.
В книге Б: доказали теорему 2, а из нее теорему 1.А теперь задумайтесь, что получается, если вы решили взять, скажем, доказательство теоремы 1 из книжки Б, а доказательство теоремы 2 из книжки А… Впрочем, если вы решили, что вам не сильно-то интересны и нужны доказательства и строгое пирамидное развитие теории, то это может быть не так уж страшно, кроме того, что породит у вас искаженное представление о “действительности”. Тут же замечу, что полностью игнорировать изучение доказательств так себе идея ввиду того, что некоторые из них используют приёмы и идеи, полезные для решения задач. А нас же в конечном итоге интересует совершенствование в этом плане, да?)
-
Конечно же, учитывая всё вышесказанное, выбирать стоит из предложенного того автора, чье изложение материала показалось вам ближе всего (т.е. понятнее и доступнее). Для определения фаворита можно почитать одну и ту же тему в разных учебниках и прислушаться к себе 😉
-
И специально для студентов ВУЗов: С БОЛЬШОЙ ОСТОРОЖНОСТЬЮ ПОЛЬЗУЙТЕСЬ “МЕТОДИЧКАМИ” от старшекурсников. Обязательно сверяйтесь с учебниками касательно написанного. Потому как это тот тип литературы, который просто кишит неточностями, ошибками и совсем уж невероятными фактами. Их можно читать только уже разобравшись в предмете, как научпоп или фантастику.
Впрочем, всё изложенное выше можно отнести не только к математическому анализу, но и к любой другой математической дисциплине (а может, и не только математической, вот за это не ручаюсь).
Второй момент, который оказывается на первом курсе затруднительным, это гениальный аппарат – “эпсилон-дельта определения” и иже с ними. Определения, заключающие в себе набор символов, среди которых понакиданы кванторы (порой до 3х разных типов в одной математической “фразе”!) вперемежку с множествами/пространствами, их элементами и еще бог знает чем вызывают нереальные трудности при запоминании! Что очень часто демонстрируют студенты на коллоквиумах, зачётах, экзаменах… Кто виноват? И что делать?
Ответ прост и сложен одновременно – не механически “заучивать” (я искренне считаю, что просто запомнить такой объём информации нереально, да и излишне), а попробовать ПОНЯТЬ, “что хотел сказать автор”. Понять, почему темы изучаются именно в таком порядке, обычно это обусловлено некоторой логикой усложнения понятий. Собственно, за что обожаю математику: объём информации, требуемой к запоминанию, выгодно отличается от гуманитарных направлений 🙂 Если вы понимаете, “чувствуете”, что там происходит, можете сами написать на математическом языке нужное определение или вывести нужное утверждение, вам становится гораздо, нет, не так, ГОРАЗДО легче!
Хорошо, тезис, думаю, ясен, а как понять-то? Приведу парочку лайфхаков:
-
Раз уж мы начали с “эпсилон-дельта определений” и аналогичного, то давайте про них и поговорим. Первое, что вам может помочь – попробуйте попереставлять кванторы всевозможными способами или заменить их на другие, “забыть” вовсе (одним словом, смоделировать реальный ответ недоучившего на экзамене), и посмотреть, что из этого получится. Возможно ли подобрать такой объект? а если возможно, то будет ли это то, чего нам хотелось изначально?
Например, вы пытаетесь разобраться с критерием Коши сходимости последовательности. Один из вариантов написания условия Коши фундаментальности последовательности {xk} k ∈ N выглядит так:
Что будет, если мы переставим один из кванторов в начало? То есть
Даст ли нам это сходящуюся последовательность? Или нет?
-
Второй лайфхак удаётся применить не везде, но тоже довольно важен – это попытка понять, а есть ли геометрическая или физическая интерпретация того или иного понятия/свойства? Эти интерпретации также порой помогают понять, возможно ли то, про что спрашивают в задаче, что вероятнее: обладает функция тем или иным свойством или нет?
Например, производная одномерной функции (можно считать, что от времени) – это мгновенная скорость траектории точки в данный момент времени. Может ли точка начать движение с положительной скоростью, двигаться гладко, сменить скорость на отрицательную, обойдя стороной момент остановки? А что для функции означает то, что она непрерывна? А равномерно непрерывна?
-
Большое количество утверждений с самыми разными требованиями к объектам в них тоже могут вызывать затруднения. Как помочь себе запомнить, что где требовать? Да и вообще, какие из условий являются техническими (т.е. без них доказательство становится в разы сложнее), а какие по существу (то есть выкину и всё, найдётся контрпример)? Хороший способ – попробовать повыкидывать условия и попридумывать контрпримеры.
Пример. Рассматриваете теорему об обратной функции. Самый простой вариант: вам дают функцию на отрезке и требуют там её непрерывности и строгой монотонности. Что будет, если убрать одно из условий? Всегда ли получится ввести обратную функцию? А бывают ли функции, не удовлетворяющие одному из условий, но тем не менее имеющие обратную?
-
Этот момент в целом можно было озвучить еще при обсуждении литературы, но мне захотелось его выделить особенно, так как на мой взгляд он архиважен. А именно:
при изучении утверждений обращайте внимания на принятые в соответствующем источнике определения объектов и обозначения. Под словом “гладкая” могут скрываться функции разной степени “хорошести”, или, например, у одного автора в утверждении дополнительно указано, что функция должна быть ограничена, у другого нет, кто прав? Да, возможно, оба, просто один понимает, скажем, интеграл Римана как предел интегральных сумм, и тогда ограниченность функции – необходимое условие интегрируемости, а другой ввёл его через суммы Дарбу, для чего ограниченность пришлось “вшить” в определение. И тогда в утверждении вновь подчеркивать ограниченность нет никакой нужды. Оба определения при этом приводят к рассмотрению одного и того же объекта в итоге, но чисто формально утверждения будут отличаться. Отличная ловушка для читателя!
На этом на сегодня всё, удачи вам в познании!
P.S. И не расстраивайтесь, если при применении некоторых лайфхаков поставите себе задачи, на которые не получается дать ответы, да и даже загуглить не удаётся – это нормально, порой задачам надо дать время осесть… или же обсудить с товарищами по несчастью 🙂 Или же просто отпустить (ситуацию)).
P.P.S. Ответы на вопросы в тексте:
-
Критерий Коши. Нет, не даст. Рассмотрите последовательность
или
.
-
Про точку: нет, не может (теорема о нулях функции).
Непрерывность в точке: при рассмотрении графика исследуемой функции получается, что сколь малый эпсилон мы бы ни взяли (это будет половиной высоты прямоугольника без границы, который мы строим, отступив вверх и вниз от уровня, равного значению функции в рассматриваемой точке), для него всегда найдётся дельта (половина ширины прямоугольника), такое что, взяв произвольный аргумент со стороны прямоугольника, параллельной оси абсцисс, я обнаружу, что значение функции в этом аргументе попадает во внутрь построенного прямоугольника. В равномерной непрерывности мы построение чуть видоизменяем: выбрать дельта можно так, что прямоугольник со сторонами дельта и эпсилон можно двигать по всему множеству, на котором функция претендует на равномерную непрерывность, и при этом функция не будет пересекать стороны прямоугольника, параллельные оси абсцисс. -
Не всегда, рассмотрите функцию
Существуют:
на отрезке [−1; 1].
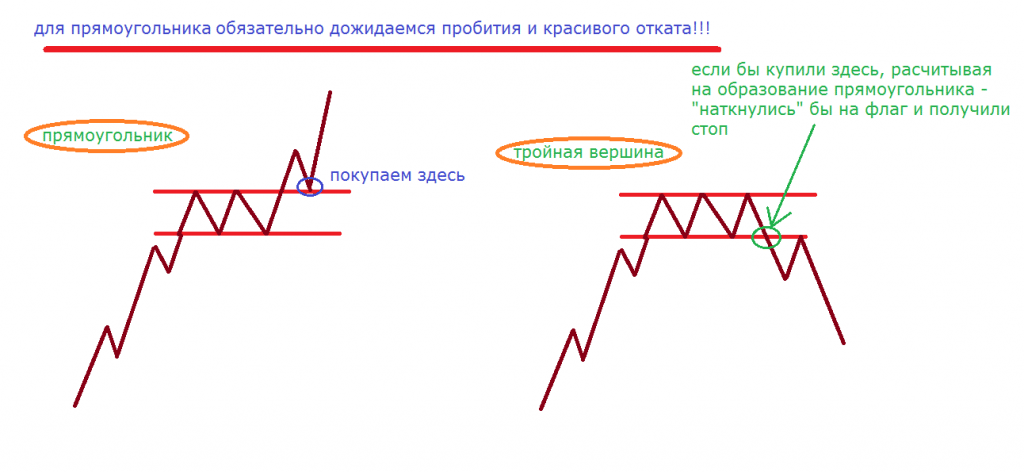
Прямоугольник в трейдинге – что это такое, как выглядит на графике, стратегии торгов.
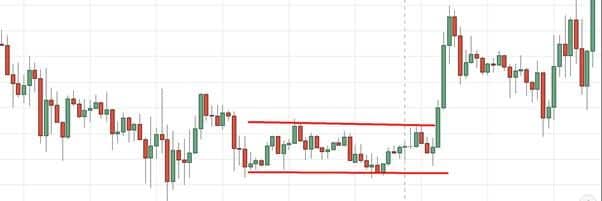
Прямоугольник в трейдинге – одна из наиболее известных и популярных фигур. На нее ориентируются трейдеры, торгующие на самых разных рынках.
Видя на графике паттерн прямоугольник, трейдер может понять, что в данный момент участники торгов настроены нерешительно, но рано или поздно этот период закончится и тренд продолжит свое движение в заданном направлении.
Содержание
- Как вычислить фигуру прямоугольник на графике – правильная интерпретация
- Составляющие элементы фигуры “прямоугольник”
- Виды “прямоугольника”
- Бычий паттерн
- Медвежий паттерн
- Как использовать фигуру прямоугольник в техническом анализе трейдерам
- Плюсы и минусы паттерна
- Ошибки и риски
- Мнение специалистов
Как вычислить фигуру прямоугольник на графике – правильная интерпретация
На графике интерпретировать прямоугольник достаточно легко. Он выглядит, как боковой коридор, консолидирующий график цены и ограниченный уровнями поддержки и сопротивления.
Обычно паттерн начинается с того, что цена упирается в уровень сопротивления, если тренд восходящий или в уровень поддержки, если нисходящий. Далее происходит откат цены до противоположного уровня. После этого цена оказывается в канале между двумя уровнями и движется в нем, пока наконец не пробьет один из них.
До того момента, пока цена не пробила уровень и очередная свеча не закрылась за пределами канала, говорить о завершении паттерна нельзя. При этом чем уже прямоугольник, тем с большим импульсом цена пробивает уровень.
Свечные формации в трейдинге – паттерны продолжения и разворота тренда
Кстати, не всегда прямоугольник выступает как самостоятельная фигура. Очень часто он является составляющей другого известного паттерна – флага.
Флаг можно определить благодаря тому, что прямоугольнику предшествует длинный восходящий или же нисходящий импульс, достигающий уровня поддержки или сопротивления (в зависимости от тренда).
В дальнейшем цена консолидируется между уровнями и колеблется до самого пробоя, который, как правило, продолжает тенденцию, заданную первоначальным импульсом.
Составляющие элементы фигуры “прямоугольник”
Прямоугольник в трейдинге состоит из “пиков” и “падений”. Их не должно быть меньше трех, хотя некоторые аналитики начинают считать паттерн прямоугольник в трейдинге таковым после двух отскоков.
Максимальное количество таких точек никак не ограничено. Однако опытные трейдеры знают, что их не будет очень много. Обычно цена несколько раз касается линий ограничения, а после пробивает их.
А что с объемами? Можно заметить, что по мере формирования прямоугольника объемы постепенно снижаются, к моменту завершения паттерна объем может и вовсе достигнуть минимума.
Пробой обычно сопровождается резким ростом объемов. Если же пробой произошел, а объемы не выросли, велик шанс, что пробой был ложный. Однако ориентироваться только на объемы при вычислении истинного или ложного пробоя не стоит. Часто бывает, что успешный пробой не сопровождается значимыми изменениями объемов, поэтому лучше ориентироваться сразу на несколько показателей.
Виды “прямоугольника”
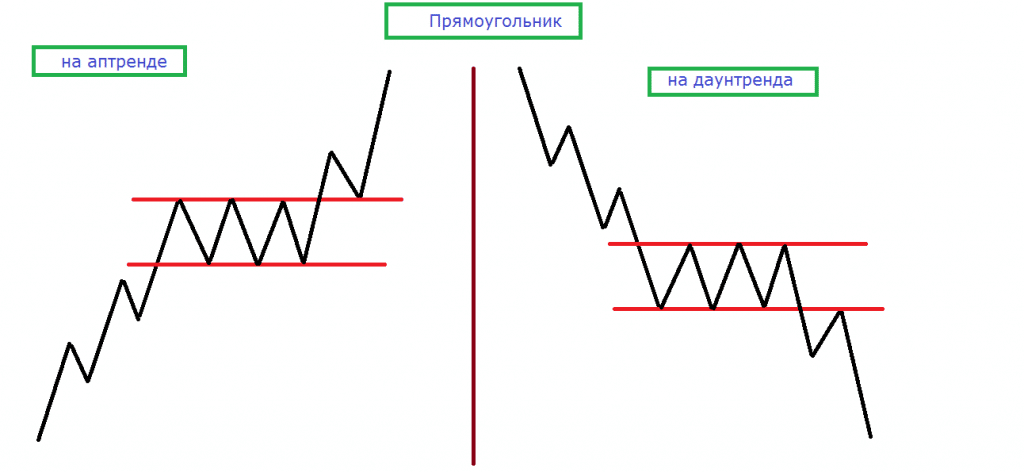
В зависимости от восходящего или нисходящего тренда прямоугольник может быть бычьим или медвежьим, соответственно.
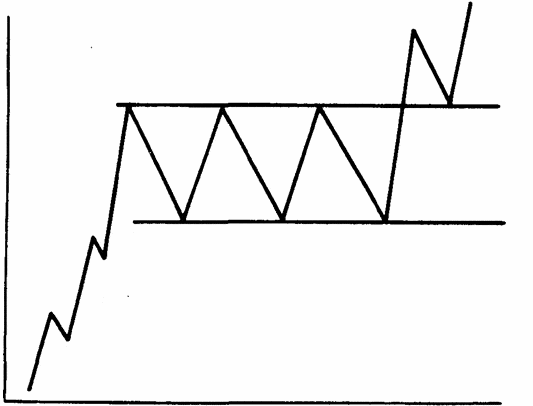
Бычий паттерн
Бычий прямоугольник в трейдинге формируется при нисходящем тренде. В этом случае трейдеры, торгующие по бычьей стратегии стремятся открыть лонг, чтобы закрыть позицию после того, как произойдет прорыв линии сопротивления.
Медвежий паттерн
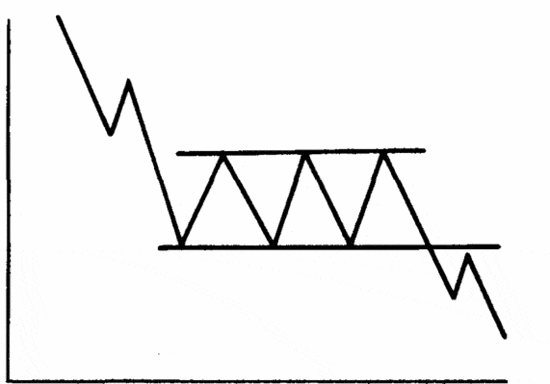
В этой ситуации все наоборот, трейдеры, занимающие медвежью позицию, стремятся открыть шорты и ждут, когда цена пробьет линию поддержки. Соответственно, медвежий прямоугольник в трейдинге образуется при нисходящем тренде.
Как использовать фигуру прямоугольник в техническом анализе трейдерам
Использовать паттерн прямоугольник в техническом анализе достаточно просто.
Для начала стоит понять какой тренд предшествовал его формированию – восходящий или нисходящий. Также стоит посмотреть нет ли на графике других, более значительных паттернов. Следующим шагом будет определение линий поддержки и сопротивления. Это несложно сделать отметив максимумы и минимумы цены внутри фигуры.
Далее трейдеру достаточно дождаться пробития. Чтобы точно быть уверенным в том, что оно состоялось, желательно дополнительно использовать осцилляторы. Точкой входа в позицию станет закрытие “пробивной” свечи.
Конечно, существуют и другие способы торговли “по прямоугольнику” отличающиеся в зависимости от общей торговой стратегии.
Основы и методы технического анализа в трейдинге – обучение для начинающих
А стоит ли торговать внутри паттерна? На этот счет у экспертов не сложилось какого-либо единого мнения. На самом деле, каждый случай достаточно индивидуальный. Если диапазон между самой высокой и низкой ценой небольшой, то особого смысла торговли внутри прямоугольника нет. Кроме тех случаев, конечно, когда трейдеру не интересен какой-нибудь скальпинг.
Если же разница между уровнем поддержки и сопротивления существенная, а паттерн развивается достаточно долгое время, то торговать внутри него вполне можно. Для этого стоит придерживаться правил торговли при боковом тренде.
Плюсы и минусы паттерна
Прямоугольник – популярная фигура в трейдинге. Этим он обязан ряду своих ключевых преимуществ:
- Его можно встретить на любых рынках: фондовых, валютных и каких-либо еще. Фигура абсолютно универсальна.
- Паттерн прямоугольник в трейдинге всегда легко распознать на графике, как правило, он сразу же бросается в глаза, с этим может справиться даже неопытный новичок.
- Фигура не только легко узнаваема, с ней еще и достаточно просто работать, не обладая особыми дополнительными знаниями и навыками. Найти точки для открытия и закрытия позиции несложно для любого трейдера, неважно торгует он в “лонг” или в “шорт”.

А есть ли недостатки у этой фигуры? К сожалению, да. Основной ее недостаток – это всегда существующий риск ложных пробоев. Если трейдер не умеет определять их на графике, то использование прямоугольника может привести его даже к убыткам.
Другой недостаток прямоугольника связан с тем, что он работает хорошо только на относительно длинных таймфреймах. Тем, кто предпочитает торговать на коротких временных промежутках, прямоугольник не принесет особой пользы.
Ошибки и риски
С чем могут быть связаны ошибки при торговле с использованием прямоугольника? Большинство из них относятся к ложному определению пробоя и, как следствие, неправильного выбора момента для открытия позиции. Для того, чтобы избежать этого достаточно воспользоваться признаками ложного пробоя, как то высокими объемами в теле прямоугольника, свечами с длинными фитилями.
Еще один момент, о котором следует помнить, это то, что прямоугольник далеко не всегда остается привязанным к изначальному импульсу и тренду. Часто, если фигура формируется достаточно долго, первичный импульс уже не оказывает на неё существенного влияния. А значит, пробой может состояться в любую сторону, независимо от изначального тренда.
Для прямоугольника свойственны также и общие риски паттернов в трейдинге. Тут стоит понимать, что паттерны не работают в отрыве от торговой стратегии. Так же, как за любым другим паттерном, за прямоугольником стоит определенная логика рынка, поведения продавцов и покупателей. Если трейдер видит всего лишь геометрическую фигуру, то он не сможет удачно использовать паттерн.
Прямоугольник в трейдинге – стратегии торгов:
Мнение специалистов
Эксперты придерживаются разных позиций, касаемо использования прямоугольника в торговле.
Джон Мерфи рекомендует не бояться торговать внутри фигуры. Он объясняет это меньшими рисками, с которыми сталкивается трейдер в этом случае, цена все равно ограничена линиями консолидации. Даже если произойдет пробой, у трейдера всегда останется возможность торговать в направлении тренда.
Александр Элдер советовал при торговле внутри прямоугольника пользоваться стратегией отскока цены от его граней.
Он утверждал, что во время консолидации цены можно открывать неплохие краткосрочные позиции. Элдер предлагал покупать у линии поддержки и продавать, когда линия цена достигнет уровня сопротивления, чтобы понять, что это действительно произошло, он советовал использовать осцилляторы или другие индикаторы.
Также, чтобы не ошибиться в будущем тренде, Элдер предлагал обращаться к более старшим таймфреймам.

А вот Джек Швагер не рекомендует торговать внутри прямоугольника. Все внимание эксперт рекомендует сосредоточить на поиске позиций на пробой. Одним из главных признаков близящегося пробоя он называет временной фактор.
Чем дольше существует паттерн, тем выше шанс, что он скоро закончится. Сигналом к пробою он также называет снижение волатильности внутри фигуры. Для снижения рисков Швагер советует дождаться подтверждения пробоя и не открывать позиции, пока эти подтверждения не появятся.