Что может быть причиной случайной ошибки измерения

Случайная
погрешность

– это составляющая
погрешности измерения, проявляющаяся
в виде непредсказуемых отклонений от
истинного значения физической величины,
меняющихся от одного наблюдения к
другому. Данная погрешность обусловлена
влиянием на результаты измерения
множества факторов, воздействие которых
на каждое отдельное измерение невозможно
учесть или заранее предсказать. Такими
причинами могут быть перепады напряжения
в сети, вибрация установки, изменения
атмосферного давления, температуры,
электрических, магнитных и радиационных
полей, а также ошибки, связанные с
действиями самого экспериментатора
(неправильное считывание показаний
приборов, различная скорость реакции
и т. п.).
Случайную погрешность нельзя исключить
из результатов измерений, однако,
пользуясь статистическими методами,
можно учесть её влияние на оценку
истинного значения измеряемой величины.

В процессе измерения
оба вида погрешностей проявляются
одновременно, и погрешность измерения
можно представить в виде суммы:

изм
= 
+ 

где 
— случайная, а 
— систематическая погрешности.

Полная погрешность
измерения, являющаяся суммой указанных
составляющих, может быть представлена
в абсолютном, относительном или
нормированном виде.

Абсолютная
погрешность
– это погрешность измерения, выраженная
в единицах измеряемой величины. Наряду
с абсолютной погрешностью часто
используется термин абсолютное
значение погрешности,
под которым понимают значение погрешности
без учета ее знака. Эти два понятия
различны.

Абсолютная
погрешность
определяется как разность

или

Относительная
погрешность
– это погрешность измерения, выраженная
отношением абсолютной погрешности к
результату измерения:

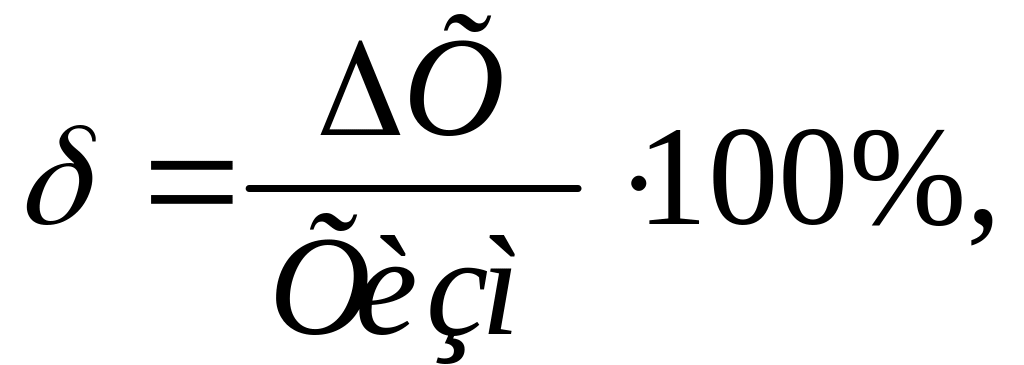
Приведенная
погрешность
– это погрешность, выраженная отношением
абсолютной погрешности средства
измерения (приборной погрешности) к
некоторой постоянной величине, называемой
нормирующим
значением
и имеющей размерность измеряемой
величины.

γ = ± (Δ/x_N
)100%,

где
x_N
– нормированное значение величины. В
качестве нормирующего множителя может
выступать, например, максимальное
значение шкалы прибора (верхний предел
показаний прибора). Понятие
приведенной погрешности относится
только к средствам измерений.

3.4 Грубые погрешности и промахи. Статические и динамические погрешности

Погрешности,
которые нельзя отнести ни к случайным,
ни к систематическим из-за совершенно
иного механизма образования и принципиально
отличного значения, называют грубыми
погрешностями измерений
или промахами.

Грубая
погрешность
– погрешность измерения, значительно
превышающая погрешности большинства
результатов наблюдений. Такие погрешности
могут возникать вследствие резкого
изменения внешних условий эксперимента:
внезапного изменения температуры,
напряжения в сети и т. п. Грубые
погрешности обнаруживают статистическими
методами и соответствующие результаты
измерений, как не отражающие
закономерностей поведения измеряемой
величины, исключают из рассмотрения.

Промах
– это вид грубой погрешности, зависящий
от наблюдателя и связанный с
неправильным обращением со средствами
измерений: неверными отсчетами показаний
приборов, описками при записи результатов,
невнимательностью экспериментатора,
путаницей номеров образцов и т. п. Промахи
обнаруживают нестатистическими методами
и результаты наблюдений, содержащие
промахи, как заведомо неправильные,
исключают из рассмотрения. Указанные
составляющие, как правило, не зависят
друг от друга, что допускает их
раздельное рассмотрение.

Очевидно, что
причинами возникновения грубой
погрешности могут быть промах оператора
при снятии отсчета или его записи, ошибка
в реализации методики измерений, сбой
в измерительной цепи прибора или
незамеченное импульсное изменение
влияющей физической величины. Причины
появления результатов с грубыми
погрешностями резко выпадают из ряда
механизмов, формирующих систематические
или случайные составляющие погрешности
измерений.

В зависимости от
режима измерения погрешности
принято делить на
статические и динамические. Статическая
погрешность измерений
(статическая погрешность) – погрешность
результата измерений, свойственная
условиям статического измерения.
Динамическая
погрешность измерений
(динамическая погрешность) –
погрешность
результата измерений, свойственная
условиям динамического измерения.

Динамической
погрешностью средства измерений
называется составляющая
погрешности, дополнительная к статической,
и возникающая при измерении в динамическом
режиме. В
соответствии с определением

где

– динамическая погрешность средства
измерения;

– погрешность
средства измерения при использовании
его в динамическом режиме;

– статическая
погрешность средства измерения
(погрешность при использовании средства
измерений в статическом режиме).

Логически
обоснованной представляется следующая
укрупненная классификация
погрешностей измерений по степени
полноты информации об
их характере и значениях:

определенные
погрешности,
неопределенные
погрешности.

К определенным
можно отнести любые известные по
числовому значению и знаку погрешности.
Известными могут стать, например те
составляющие погрешности измерений,
которые имеют достаточно жесткую
функциональную связь с вызывающими их
аргументами. Такие погрешности по сути
совпадают с систематическими и
принципиально могут быть выявлены и
исключены из результатов измерений, их
значения можно прогнозировать.
Определенной можно считать также любую
(в том числе и уже зафиксированную
случайную или даже грубую) погрешность,
числовое значение и знак которой получены
экспериментальными методами.

Определенные
погрешности в при достаточной полноте
информации могут быть исключены из
результатов измерений. Теоретическая
определенность систематических
погрешностей делает возможным исключение
этих погрешностей до измерений, в
процессе измерений, а также при
математической обработке результатов
измерительного эксперимента после
выполнения измерений.

К неопределенным
погрешностям следует отнести невыявленные
систематические, а также погрешности
случайные (собственно случайные) и
грубые погрешности, значения которых
не были определены экспериментально.
При исключении определенных погрешностей
абсолютная точность невозможна, поэтому
приходится относить к неопределенным
неисключенные остатки погрешностей.

Неисключенная
систематическая погрешность
– составляющая
погрешности результата измерений,
обусловленная погрешностями вычисления
и введения поправок на влияние
систематических погрешностей или
систематической погрешностью, поправка
на действие которой не введена вследствие
ее малости .

Систематическими
составляющими, значения которых
существенно меньше случайных погрешностей
(
),
пренебрегают. Такие погрешности относят
к пренебрежимо малым неисключенным
систематическим составляющим погрешности
измерения.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

Свойства физического объекта (явления, процесса) определяются набором
количественных характеристик — физических величин.
Как правило, результат измерения представляет
собой число, задающее отношение измеряемой величины к некоторому эталону.
Сравнение с эталоном может быть как
прямым (проводится непосредственно
экспериментатором), так и косвенным (проводится с помощью некоторого
прибора, которому экспериментатор доверяет).
Полученные таким образом величины имеют размерность, определяемую выбором эталона.

Замечание. Результатом измерения может также служить количество отсчётов некоторого
события, логическое утверждение (да/нет) или даже качественная оценка
(сильно/слабо/умеренно). Мы ограничимся наиболее типичным для физики случаем,
когда результат измерения может быть представлен в виде числа или набора чисел.

Взаимосвязь между различными физическими величинами может быть описана
физическими законами, представляющими собой идеализированную
модель действительности. Конечной целью любого физического
эксперимента (в том числе и учебного) является проверка адекватности или
уточнение параметров таких моделей.

1.1 Результат измерения

Рассмотрим простейший пример: измерение длины стержня
с помощью линейки. Линейка проградуирована производителем с помощью
некоторого эталона длины — таким образом, сравнивая длину
стержня с ценой деления линейки, мы выполняем косвенное сравнение с
общепринятым стандартным эталоном.

Допустим, мы приложили линейку к стержню и увидели на шкале некоторый результат
x=xизм. Можно ли утверждать, что xизм — это длина
стержня?

Во-первых, значение x не может быть задано точно, хотя бы
потому, что оно обязательно округлено до некоторой значащей
цифры: если линейка «обычная», то у неё
есть цена деления; а если линейка, к примеру, «лазерная»
— у неё высвечивается конечное число значащих цифр
на дисплее.

Во-вторых, мы никак не можем быть уверенны, что длина стержня на
самом деле такова хотя бы с точностью до ошибки округления. Действительно,
мы могли приложить линейку не вполне ровно; сама линейка могла быть
изготовлена не вполне точно; стержень может быть не идеально цилиндрическим
и т.п.

И, наконец, если пытаться хотя бы гипотетически переходить к бесконечной
точности измерения, теряет смысл само понятие «длины стержня». Ведь
на масштабах атомов у стержня нет чётких границ, а значит говорить о его
геометрических размерах в таком случае крайне затруднительно!

Итак, из нашего примера видно, что никакое физическое измерение не может быть
произведено абсолютно точно, то есть
у любого измерения есть погрешность.

Замечание. Также используют эквивалентный термин ошибка измерения
(от англ. error). Подчеркнём, что смысл этого термина отличается от
общеупотребительного бытового: если физик говорит «в измерении есть ошибка»,
— это не означает, что оно неправильно и его надо переделать.
Имеется ввиду лишь, что это измерение неточно, то есть имеет
погрешность.

Количественно погрешность можно было бы определить как разность между
измеренным и «истинным» значением длины стержня:
δ⁢x=xизм-xист. Однако на практике такое определение
использовать нельзя: во-первых, из-за неизбежного наличия
погрешностей «истинное» значение измерить невозможно, и во-вторых, само
«истинное» значение может отличаться в разных измерениях (например, стержень
неровный или изогнутый, его торцы дрожат из-за тепловых флуктуаций и т.д.).
Поэтому говорят обычно об оценке погрешности.

Об измеренной величине также часто говорят как об оценке, подчеркивая,
что эта величина не точна и зависит не только от физических свойств
исследуемого объекта, но и от процедуры измерения.

Замечание.
Термин оценка имеет и более формальное значение. Оценкой называют результат процедуры получения значения параметра или параметров физической модели, а также иногда саму процедуру. Теория оценок является подразделом математической статистики. Некоторые ее положения изложены в главе 3, но для более серьезного понимания следует обратиться к [5].

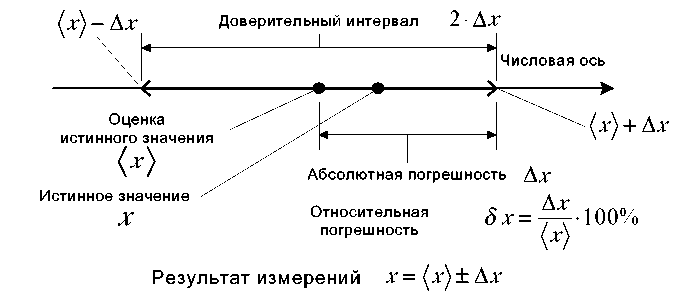
Для оценки значения физической величины корректно использовать
не просто некоторое фиксированное число xизм, а интервал (или
диапазон) значений, в пределах которого может лежать её
«истинное» значение. В простейшем случае этот интервал
может быть записан как

где δ⁢x — абсолютная величина погрешности.
Эта запись означает, что исследуемая величина лежит в интервале
x∈(xизм-δ⁢x;xизм+δ⁢x)
с некоторой достаточно большой долей вероятности (более подробно о
вероятностном содержании интервалов см. п. 2.2).
Для наглядной оценки точности измерения удобно также использовать
относительную величину погрешности:

Она показывает, насколько погрешность мала по сравнению с
самой измеряемой величиной (её также можно выразить в процентах:
ε=δ⁢xx⋅100%).

Пример. Штангенциркуль —
прибор для измерения длин с ценой деления 0,1⁢мм. Пусть
диаметр некоторой проволоки равен 0,37 мм. Считая, что абсолютная
ошибка составляет половину цены деления прибора, результат измерения
можно будет записать как d=0,40±0,05⁢мм (или
d=(40±5)⋅10-5⁢м).
Относительная погрешность составляет ε≈13%, то
есть точность измерения весьма посредственная — поскольку
размер объекта близок к пределу точности прибора.

О необходимости оценки погрешностей.

Измерим длины двух стержней x1 и x2 и сравним результаты.
Можно ли сказать, что стержни одинаковы или различны?

Казалось бы,
достаточно проверить, справедливо ли x1=x2. Но никакие
два результата измерения не равны друг другу с абсолютной точностью! Таким
образом, без указания погрешности измерения ответ на этот вопрос дать
невозможно.

С другой стороны, если погрешность δ⁢x известна, то можно
утверждать, что если измеренные длины одинаковы
в пределах погрешности опыта, если |x2-x1|<δ⁢x
(и различны в противоположном случае).

Итак, без знания погрешностей невозможно сравнить между собой никакие
два измерения, и, следовательно, невозможно сделать никаких
значимых выводов по результатам эксперимента: ни о наличии зависимостей
между величинами, ни о практической применимости какой-либо теории,
и т. п. В связи с этим задача правильной оценки погрешностей является крайне
важной, поскольку существенное занижение или завышение значения погрешности
(по сравнению с реальной точностью измерений) ведёт к неправильным выводам.

В физическом эксперименте (в том числе лабораторном практикуме) оценка
погрешностей должна проводиться всегда
(даже когда составители задания забыли упомянуть об этом).

1.2 Многократные измерения

Проведём серию из n одинаковых (однотипных) измерений одной
и той же физической величины (например, многократно приложим линейку к стержню) и получим
ряд значений

Что можно сказать о данном наборе чисел и о длине стержня?
И можно ли увеличивая число измерений улучшить конечный результат?

Если цена деления самой линейки достаточно мала, то как нетрудно убедиться
на практике, величины {xi} почти наверняка окажутся
различными. Причиной тому могут быть
самые разные обстоятельства, например: у нас недостаточно остроты
зрения и точности рук, чтобы каждый раз прикладывать линейку одинаково;
стенки стержня могут быть слегка неровными; у стержня может и не быть
определённой длины, например, если в нём возбуждены звуковые волны,
из-за чего его торцы колеблются, и т. д.

В такой ситуации результат измерения интерпретируется как
случайная величина, описываемая некоторым вероятностным законом
(распределением).
Подробнее о случайных величинах и методах работы с ними см. гл. 2.

По набору результатов 𝐱 можно вычислить их среднее арифметическое:

⟨x⟩=x1+x2+…+xnn≡1n⁢∑i=1nxi.

(1.1)

Это значение, вычисленное по результатам конечного числа n измерений,
принято называть выборочным средним. Здесь и далее для обозначения
выборочных средних будем использовать угловые скобки.

Кроме среднего представляет интерес и то, насколько сильно варьируются
результаты от опыта к опыту. Определим отклонение каждого измерения от среднего как

Разброс данных относительно среднего принято характеризовать
среднеквадратичным отклонением:

s=Δ⁢x12+Δ⁢x22+…+Δ⁢xn2n=1n⁢∑i=1nΔ⁢xi2

(1.2)

или кратко

Значение среднего квадрата отклонения s2 называют
выборочной дисперсией.

Будем увеличивать число измерений n (n→∞). Если объект измерения и методика
достаточно стабильны, то отклонения от среднего Δ⁢xi будут, во-первых,
относительно малы, а во-вторых, положительные и отрицательные отклонения будут
встречаться примерно одинаково часто. Тогда при вычислении (1.1)
почти все отклонения Δ⁢xi скомпенсируются и можно ожидать,
что выборочное среднее при n≫1 будет стремиться к некоторому пределу:

Тогда предельное значение x¯ можно отождествить с «истинным» средним
для исследуемой величины.

Предельную величину среднеквадратичного отклонения при n→∞
обозначим как

Замечание. В общем случае указанные пределы могут и не существовать. Например, если измеряемый параметр
меняется во времени или в результате самого измерения, либо испытывает слишком большие
случайные скачки и т. п. Такие ситуации требуют особого рассмотрения и мы на них не
останавливаемся.

Замечание. Если n мало (n<10), для оценки среднеквадратичного отклонения
математическая статистика рекомендует вместо формулы (1.3) использовать
исправленную формулу (подробнее см. п. 5.2):

sn-12=1n-1⁢∑i=1nΔ⁢xi2,

(1.4)

где произведена замена n→n-1. Величину sn-1
часто называют стандартным отклонением.

Итак, можно по крайней мере надеяться на то, что результаты небольшого числа
измерений имеют не слишком большой разброс, так что величина ⟨x⟩
может быть использована как приближенное значение (оценка) истинного значения
⟨x⟩≈x¯,
а увеличение числа измерений позволит уточнить результат.

Многие случайные величины подчиняются так называемому нормальному закону
распределения (подробнее см. Главу 2). Для таких величин
могут быть строго доказаны следующие свойства:

•

при многократном повторении эксперимента бо́льшая часть измерений
(∼68%) попадает в интервал x¯-σ<x<x¯+σ
(см. п. 2.2).
•

выборочное среднее значение ⟨x⟩ оказывается с большей
вероятностью ближе к истинному значению x¯, чем каждое из измерений
{xi} в отдельности. При этом ошибка вычисления среднего
убывает пропорционально корню из числа опытов n
(см. п. 2.4).

Упражнение. Показать, что

s2=⟨x2⟩-⟨x⟩2.

(1.5)

то есть дисперсия равна разности среднего значения квадрата
⟨x2⟩=1n⁢∑i=1nxi2
и квадрата среднего ⟨x⟩2=(1n⁢∑i=1nxi)2.

1.3 Классификация погрешностей

Чтобы лучше разобраться в том, нужно ли многократно повторять измерения,
и в каком случае это позволит улучшить результаты опыта,
проанализируем источники и виды погрешностей.

В первую очередь, многократные измерения позволяют проверить
воспроизводимость результатов: повторные измерения в одинаковых
условиях, должны давать близкие результаты. В противном случае
исследование будет существенно затруднено, если вообще возможно.
Таким образом, многократные измерения необходимы для того,
чтобы убедиться как в надёжности методики, так и в существовании измеряемой
величины как таковой.

При любых измерениях возможны грубые ошибки — промахи
(англ. miss). Это «ошибки» в стандартном
понимании этого слова — возникающие по вине экспериментатора
или в силу других непредвиденных обстоятельств (например, из-за сбоя
аппаратуры). Промахов, конечно, нужно избегать, а результаты таких
измерений должны быть по возможности исключены из рассмотрения.

Как понять, является ли «аномальный» результат промахом? Вопрос этот весьма
непрост. В литературе существуют статистические
критерии отбора промахов, которыми мы, однако, настоятельно не рекомендуем
пользоваться (по крайней мере, без серьезного понимания последствий
такого отбора). Отбрасывание аномальных данных может, во-первых, привести
к тенденциозному искажению результата исследований, а во-вторых, так
можно упустить открытие неизвестного эффекта. Поэтому при научных
исследованиях необходимо максимально тщательно проанализировать причину
каждого промаха, в частности, многократно повторив эксперимент. Лишь
только если факт и причина промаха установлены вполне достоверно,
соответствующий результат можно отбросить.

Замечание. Часто причины аномальных отклонений невозможно установить на этапе
обработки данных, поскольку часть информации о проведении измерений к этому моменту
утеряна. Единственным способ борьбы с этим — это максимально подробное описание всего
процесса измерений в лабораторном журнале. Подробнее об этом
см. п. 4.1.1.

При многократном повторении измерении одной и той же физической величины
погрешности могут иметь систематический либо случайный
характер. Назовём погрешность систематической, если она повторяется
от опыта к опыту, сохраняя свой знак и величину, либо закономерно
меняется в процессе измерений. Случайные (или статистические)
погрешности меняются хаотично при повторении измерений как по величине,
так и по знаку, и в изменениях не прослеживается какой-либо закономерности.

Кроме того, удобно разделять погрешности по их происхождению. Можно
выделить

•

инструментальные (или приборные) погрешности,
связанные с несовершенством конструкции (неточности, допущенные при
изготовлении или вследствие старения), ошибками калибровки или ненормативными
условиями эксплуатации измерительных приборов;
•

методические погрешности, связанные с несовершенством
теоретической модели явления (использование приближенных формул и
моделей явления) или с несовершенством методики измерения (например,
влиянием взаимодействия прибора и объекта измерения на результат измерения);
•

естественные погрешности, связанные со случайным
характером
измеряемой физической величины — они являются не столько
«ошибками» измерения, сколько характеризуют
природу изучаемого объекта или явления.

Замечание. Разделение погрешностей на систематические и случайные
не является однозначным и зависит от постановки опыта. Например, производя
измерения не одним, а несколькими однотипными приборами, мы переводим
систематическую приборную ошибку, связанную с неточностью шкалы и
калибровки, в случайную. Разделение по происхождению также условно,
поскольку любой прибор подвержен воздействию «естественных»
случайных и систематических ошибок (шумы и наводки, тряска, атмосферные
условия и т. п.), а в основе работы прибора всегда лежит некоторое
физическое явление, описываемое не вполне совершенной теорией.

1.3.1 Случайные погрешности

Случайный характер присущ большому количеству различных физических
явлений, и в той или иной степени проявляется в работе всех без исключения
приборов. Случайные погрешности обнаруживаются просто при многократном
повторении опыта — в виде хаотичных изменений (флуктуаций)
значений {xi}.

Если случайные отклонения от среднего в большую или меньшую стороны
примерно равновероятны, можно рассчитывать, что при вычислении среднего
арифметического (1.1) эти отклонения скомпенсируются,
и погрешность результирующего значения ⟨x⟩ будем меньше,
чем погрешность отдельного измерения.

Случайные погрешности бывают связаны, например,

•

с особенностями используемых приборов: техническими
недостатками
(люфт в механических приспособлениях, сухое трение в креплении стрелки
прибора), с естественными (тепловой и дробовой шумы в электрических
цепях, тепловые флуктуации и колебания измерительных устройств из-за
хаотического движения молекул, космическое излучение) или техногенными
факторами (тряска, электромагнитные помехи и наводки);
•

с особенностями и несовершенством методики измерения (ошибка
при отсчёте по шкале, ошибка времени реакции при измерениях с секундомером);
•

с несовершенством объекта измерений (неровная поверхность,
неоднородность состава);
•

со случайным характером исследуемого явления (радиоактивный
распад, броуновское движение).

Остановимся несколько подробнее на двух последних случаях. Они отличаются
тем, что случайный разброс данных в них порождён непосредственно объектом
измерения. Если при этом приборные погрешности малы, то «ошибка»
эксперимента возникает лишь в тот момент, когда мы по своей
воле совершаем замену ряда измеренных значений на некоторое среднее
{xi}→⟨x⟩. Разброс данных при этом
характеризует не точность измерения, а сам исследуемый объект или
явление. Однако с математической точки зрения приборные и
«естественные»
погрешности неразличимы — глядя на одни только
экспериментальные данные невозможно выяснить, что именно явилось причиной
их флуктуаций: сам объект исследования или иные, внешние причины.
Таким образом, для исследования естественных случайных процессов необходимо
сперва отдельно исследовать и оценить случайные инструментальные погрешности
и убедиться, что они достаточно малы.

1.3.2 Систематические погрешности

Систематические погрешности, в отличие от случайных, невозможно обнаружить,
исключить или уменьшить просто многократным повторением измерений.
Они могут быть обусловлены, во-первых, неправильной работой приборов
(инструментальная погрешность), например, сдвигом нуля отсчёта
по шкале, деформацией шкалы, неправильной калибровкой, искажениями
из-за не нормативных условий эксплуатации, искажениями из-за износа
или деформации деталей прибора, изменением параметров прибора во времени
из-за нагрева и т.п. Во-вторых, их причиной может быть ошибка в интерпретации
результатов (методическая погрешность), например, из-за использования
слишком идеализированной физической модели явления, которая не учитывает
некоторые значимые факторы (так, при взвешивании тел малой плотности
в атмосфере необходимо учитывать силу Архимеда; при измерениях в электрических
цепях может быть необходим учет неидеальности амперметров и вольтметров
и т. д.).

Систематические погрешности условно можно разделить на следующие категории.

1.

Известные погрешности, которые могут быть достаточно точно вычислены
или измерены. При необходимости они могут быть учтены непосредственно:
внесением поправок в расчётные формулы или в результаты измерений.
Если они малы, их можно отбросить, чтобы упростить вычисления.
2.

Погрешности известной природы, конкретная величина которых неизвестна,
но максимальное значение вносимой ошибки может быть оценено теоретически
или экспериментально. Такие погрешности неизбежно присутствуют в любом
опыте, и задача экспериментатора — свести их к минимуму,
совершенствуя методики измерения и выбирая более совершенные приборы.

Чтобы оценить величину систематических погрешностей опыта, необходимо
учесть паспортную точность приборов (производитель, как правило, гарантирует,
что погрешность прибора не превосходит некоторой величины), проанализировать
особенности методики измерения, и по возможности, провести контрольные
опыты.
3.

Погрешности известной природы, оценка величины которых по каким-либо
причинам затруднена (например, сопротивление контактов при подключении
электронных приборов). Такие погрешности должны быть обязательно исключены
посредством модификации методики измерения или замены приборов.
4.

Наконец, нельзя забывать о возможности существования ошибок, о
которых мы не подозреваем, но которые могут существенно искажать результаты
измерений. Такие погрешности самые опасные, а исключить их можно только
многократной независимой проверкой измерений, разными методами
и в разных условиях.

В учебном практикуме учёт систематических погрешностей ограничивается,
как правило, паспортными погрешностями приборов и теоретическими поправками
к упрощенной модели исследуемого явления.

Точный учет систематической ошибки возможен только при учете специфики конкретного эксперимента. Особенное внимание надо обратить на зависимость (корреляцию) систематических смещений при повторных измерениях. Одна и та же погрешность в разных случаях может быть интерпретирована и как случайная, и как систематическая.

Пример.
Калибровка электромагнита производится при помощи внесения в него датчика Холла или другого измерителя магнитного потока. При последовательных измерениях с разными токами (и соотственно полями в зазоре) калибровку можно учитыать двумя различными способами:

•

Измерить значение поля для разных токов, построить линейную калибровочную кривую и потом использовать значения, восстановленные по этой кривой для вычисления поля по току, используемому в измерениях.

•

Для каждого измерения проводить допольнительное измерения поля и вообще не испльзовать значения тока.

В первом случае погрешность полученного значения будет меньше, поскльку при проведении прямой, отдельные отклонения усреднятся. При этом погрешность измерения поля будет носить систематический харрактер и при обработке данных ее надо будет учитывать в последний момент. Во втором случае погрешность будет носить статистический (случайный) харрактер и ее надо будет добавить к погрешности каждой измеряемой точки. При этом сама погрешность будет больше. Выбор той или иной методики зависит от конретной ситуации. При большом количестве измерений, второй способ более надежный, поскольку статистическая ошибка при усреднении уменьшается пропорционально корню из количества измерений. Кроме того, такой способ повзоляет избежать методической ошибки, связанной с тем, что зависимость поля от тока не является линейной.

Пример.
Рассмотрим измерение напряжения по стрелочному вольтметру. В показаниях прибора будет присутствовать три типа погрешности:

1.

Статистическая погрешность, связанная с дрожанием стрелки и ошибкой визуального наблюдения, примерно равная половине цены деления.

2.

Систематическая погрешность, связанная с неправильной установкой нуля.

3.

Систематическая погрешность, связанная с неправильным коэффициентом пропорциональности между напряжением и отклонением стрелки. Как правило приборы сконструированы таким образом, чтобы максимальное значение этой погрешности было так же равно половине цены деления (хотя это и не гарантируется).

Источник

From Wikipedia, the free encyclopedia

«Systematic bias» redirects here. For the sociological and organizational phenomenon, see Systemic bias.

Observational error (or measurement error) is the difference between a measured value of a quantity and its true value.^[1] In statistics, an error is not necessarily a «mistake». Variability is an inherent part of the results of measurements and of the measurement process.

Measurement errors can be divided into two components: random and systematic.^[2]
Random errors are errors in measurement that lead to measurable values being inconsistent when repeated measurements of a constant attribute or quantity are taken. Systematic errors are errors that are not determined by chance but are introduced by repeatable processes inherent to the system.^[3] Systematic error may also refer to an error with a non-zero mean, the effect of which is not reduced when observations are averaged.^{[citation needed]}

Measurement errors can be summarized in terms of accuracy and precision.
Measurement error should not be confused with measurement uncertainty.

Science and experiments[edit]

When either randomness or uncertainty modeled by probability theory is attributed to such errors, they are «errors» in the sense in which that term is used in statistics; see errors and residuals in statistics.

Every time we repeat a measurement with a sensitive instrument, we obtain slightly different results. The common statistical model used is that the error has two additive parts:

Systematic error which always occurs, with the same value, when we use the instrument in the same way and in the same case.
Random error which may vary from observation to another.

Systematic error is sometimes called statistical bias. It may often be reduced with standardized procedures. Part of the learning process in the various sciences is learning how to use standard instruments and protocols so as to minimize systematic error.

Random error (or random variation) is due to factors that cannot or will not be controlled. One possible reason to forgo controlling for these random errors is that it may be too expensive to control them each time the experiment is conducted or the measurements are made. Other reasons may be that whatever we are trying to measure is changing in time (see dynamic models), or is fundamentally probabilistic (as is the case in quantum mechanics — see Measurement in quantum mechanics). Random error often occurs when instruments are pushed to the extremes of their operating limits. For example, it is common for digital balances to exhibit random error in their least significant digit. Three measurements of a single object might read something like 0.9111g, 0.9110g, and 0.9112g.

Characterization[edit]

Measurement errors can be divided into two components: random error and systematic error.^[2]

Random error is always present in a measurement. It is caused by inherently unpredictable fluctuations in the readings of a measurement apparatus or in the experimenter’s interpretation of the instrumental reading. Random errors show up as different results for ostensibly the same repeated measurement. They can be estimated by comparing multiple measurements and reduced by averaging multiple measurements.

Systematic error is predictable and typically constant or proportional to the true value. If the cause of the systematic error can be identified, then it usually can be eliminated. Systematic errors are caused by imperfect calibration of measurement instruments or imperfect methods of observation, or interference of the environment with the measurement process, and always affect the results of an experiment in a predictable direction. Incorrect zeroing of an instrument leading to a zero error is an example of systematic error in instrumentation.

The Performance Test Standard PTC 19.1-2005 “Test Uncertainty”, published by the American Society of Mechanical Engineers (ASME), discusses systematic and random errors in considerable detail. In fact, it conceptualizes its basic uncertainty categories in these terms.

Random error can be caused by unpredictable fluctuations in the readings of a measurement apparatus, or in the experimenter’s interpretation of the instrumental reading; these fluctuations may be in part due to interference of the environment with the measurement process. The concept of random error is closely related to the concept of precision. The higher the precision of a measurement instrument, the smaller the variability (standard deviation) of the fluctuations in its readings.

Sources[edit]

Sources of systematic error[edit]

Imperfect calibration[edit]

Sources of systematic error may be imperfect calibration of measurement instruments (zero error), changes in the environment which interfere with the measurement process and sometimes imperfect methods of observation can be either zero error or percentage error. If you consider an experimenter taking a reading of the time period of a pendulum swinging past a fiducial marker: If their stop-watch or timer starts with 1 second on the clock then all of their results will be off by 1 second (zero error). If the experimenter repeats this experiment twenty times (starting at 1 second each time), then there will be a percentage error in the calculated average of their results; the final result will be slightly larger than the true period.

Distance measured by radar will be systematically overestimated if the slight slowing down of the waves in air is not accounted for. Incorrect zeroing of an instrument leading to a zero error is an example of systematic error in instrumentation.

Systematic errors may also be present in the result of an estimate based upon a mathematical model or physical law. For instance, the estimated oscillation frequency of a pendulum will be systematically in error if slight movement of the support is not accounted for.

Quantity[edit]

Systematic errors can be either constant, or related (e.g. proportional or a percentage) to the actual value of the measured quantity, or even to the value of a different quantity (the reading of a ruler can be affected by environmental temperature). When it is constant, it is simply due to incorrect zeroing of the instrument. When it is not constant, it can change its sign. For instance, if a thermometer is affected by a proportional systematic error equal to 2% of the actual temperature, and the actual temperature is 200°, 0°, or −100°, the measured temperature will be 204° (systematic error = +4°), 0° (null systematic error) or −102° (systematic error = −2°), respectively. Thus the temperature will be overestimated when it will be above zero and underestimated when it will be below zero.

Drift[edit]

Systematic errors which change during an experiment (drift) are easier to detect. Measurements indicate trends with time rather than varying randomly about a mean. Drift is evident if a measurement of a constant quantity is repeated several times and the measurements drift one way during the experiment. If the next measurement is higher than the previous measurement as may occur if an instrument becomes warmer during the experiment then the measured quantity is variable and it is possible to detect a drift by checking the zero reading during the experiment as well as at the start of the experiment (indeed, the zero reading is a measurement of a constant quantity). If the zero reading is consistently above or below zero, a systematic error is present. If this cannot be eliminated, potentially by resetting the instrument immediately before the experiment then it needs to be allowed by subtracting its (possibly time-varying) value from the readings, and by taking it into account while assessing the accuracy of the measurement.

If no pattern in a series of repeated measurements is evident, the presence of fixed systematic errors can only be found if the measurements are checked, either by measuring a known quantity or by comparing the readings with readings made using a different apparatus, known to be more accurate. For example, if you think of the timing of a pendulum using an accurate stopwatch several times you are given readings randomly distributed about the mean. Hopings systematic error is present if the stopwatch is checked against the ‘speaking clock’ of the telephone system and found to be running slow or fast. Clearly, the pendulum timings need to be corrected according to how fast or slow the stopwatch was found to be running.

Measuring instruments such as ammeters and voltmeters need to be checked periodically against known standards.

Systematic errors can also be detected by measuring already known quantities. For example, a spectrometer fitted with a diffraction grating may be checked by using it to measure the wavelength of the D-lines of the sodium electromagnetic spectrum which are at 600 nm and 589.6 nm. The measurements may be used to determine the number of lines per millimetre of the diffraction grating, which can then be used to measure the wavelength of any other spectral line.

Constant systematic errors are very difficult to deal with as their effects are only observable if they can be removed. Such errors cannot be removed by repeating measurements or averaging large numbers of results. A common method to remove systematic error is through calibration of the measurement instrument.

Sources of random error[edit]

The random or stochastic error in a measurement is the error that is random from one measurement to the next. Stochastic errors tend to be normally distributed when the stochastic error is the sum of many independent random errors because of the central limit theorem. Stochastic errors added to a regression equation account for the variation in Y that cannot be explained by the included Xs.

Surveys[edit]

The term «observational error» is also sometimes used to refer to response errors and some other types of non-sampling error.^[1] In survey-type situations, these errors can be mistakes in the collection of data, including both the incorrect recording of a response and the correct recording of a respondent’s inaccurate response. These sources of non-sampling error are discussed in Salant and Dillman (1994) and Bland and Altman (1996).^[4]^[5]

These errors can be random or systematic. Random errors are caused by unintended mistakes by respondents, interviewers and/or coders. Systematic error can occur if there is a systematic reaction of the respondents to the method used to formulate the survey question. Thus, the exact formulation of a survey question is crucial, since it affects the level of measurement error.^[6] Different tools are available for the researchers to help them decide about this exact formulation of their questions, for instance estimating the quality of a question using MTMM experiments. This information about the quality can also be used in order to correct for measurement error.^[7]^[8]

Effect on regression analysis[edit]

If the dependent variable in a regression is measured with error, regression analysis and associated hypothesis testing are unaffected, except that the R² will be lower than it would be with perfect measurement.

However, if one or more independent variables is measured with error, then the regression coefficients and standard hypothesis tests are invalid.^[9]^{: p. 187} This is known as attenuation bias.^[10]

References[edit]

^ ^a ^b Dodge, Y. (2003) The Oxford Dictionary of Statistical Terms, OUP. ISBN 978-0-19-920613-1
^ ^a ^b John Robert Taylor (1999). An Introduction to Error Analysis: The Study of Uncertainties in Physical Measurements. University Science Books. p. 94, §4.1. ISBN 978-0-935702-75-0.
^ «Systematic error». Merriam-webster.com. Retrieved 2016-09-10.
^ Salant, P.; Dillman, D. A. (1994). How to conduct your survey. New York: John Wiley & Sons. ISBN 0-471-01273-4.
^ Bland, J. Martin; Altman, Douglas G. (1996). «Statistics Notes: Measurement Error». BMJ. 313 (7059): 744. doi:10.1136/bmj.313.7059.744. PMC 2352101. PMID 8819450.
^ Saris, W. E.; Gallhofer, I. N. (2014). Design, Evaluation and Analysis of Questionnaires for Survey Research (Second ed.). Hoboken: Wiley. ISBN 978-1-118-63461-5.
^ DeCastellarnau, A. and Saris, W. E. (2014). A simple procedure to correct for measurement errors in survey research. European Social Survey Education Net (ESS EduNet). Available at: http://essedunet.nsd.uib.no/cms/topics/measurement Archived 2019-09-15 at the Wayback Machine
^ Saris, W. E.; Revilla, M. (2015). «Correction for measurement errors in survey research: necessary and possible» (PDF). Social Indicators Research. 127 (3): 1005–1020. doi:10.1007/s11205-015-1002-x. hdl:10230/28341. S2CID 146550566.
^ Hayashi, Fumio (2000). Econometrics. Princeton University Press. ISBN 978-0-691-01018-2.
^ Angrist, Joshua David; Pischke, Jörn-Steffen (2015). Mastering ‘metrics : the path from cause to effect. Princeton, New Jersey. p. 221. ISBN 978-0-691-15283-7. OCLC 877846199. The bias generated by this sort of measurement error in regressors is called attenuation bias.

Science and experiments[edit]

Every time we repeat a measurement with a sensitive instrument, we obtain slightly different results. The common statistical model used is that the error has two additive parts:

Systematic error which always occurs, with the same value, when we use the instrument in the same way and in the same case.
Random error which may vary from observation to another.

Characterization[edit]

Measurement errors can be divided into two components: random error and systematic error.^[2]

Sources[edit]

Sources of systematic error[edit]

Imperfect calibration[edit]

Quantity[edit]

Drift[edit]

Measuring instruments such as ammeters and voltmeters need to be checked periodically against known standards.

Sources of random error[edit]

Surveys[edit]

Effect on regression analysis[edit]

References[edit]

^ ^a ^b Dodge, Y. (2003) The Oxford Dictionary of Statistical Terms, OUP. ISBN 978-0-19-920613-1
^ ^a ^b John Robert Taylor (1999). An Introduction to Error Analysis: The Study of Uncertainties in Physical Measurements. University Science Books. p. 94, §4.1. ISBN 978-0-935702-75-0.
^ «Systematic error». Merriam-webster.com. Retrieved 2016-09-10.
^ Salant, P.; Dillman, D. A. (1994). How to conduct your survey. New York: John Wiley & Sons. ISBN 0-471-01273-4.
^ Bland, J. Martin; Altman, Douglas G. (1996). «Statistics Notes: Measurement Error». BMJ. 313 (7059): 744. doi:10.1136/bmj.313.7059.744. PMC 2352101. PMID 8819450.
^ Saris, W. E.; Gallhofer, I. N. (2014). Design, Evaluation and Analysis of Questionnaires for Survey Research (Second ed.). Hoboken: Wiley. ISBN 978-1-118-63461-5.
^ DeCastellarnau, A. and Saris, W. E. (2014). A simple procedure to correct for measurement errors in survey research. European Social Survey Education Net (ESS EduNet). Available at: http://essedunet.nsd.uib.no/cms/topics/measurement Archived 2019-09-15 at the Wayback Machine
^ Saris, W. E.; Revilla, M. (2015). «Correction for measurement errors in survey research: necessary and possible» (PDF). Social Indicators Research. 127 (3): 1005–1020. doi:10.1007/s11205-015-1002-x. hdl:10230/28341. S2CID 146550566.
^ Hayashi, Fumio (2000). Econometrics. Princeton University Press. ISBN 978-0-691-01018-2.
^ Angrist, Joshua David; Pischke, Jörn-Steffen (2015). Mastering ‘metrics : the path from cause to effect. Princeton, New Jersey. p. 221. ISBN 978-0-691-15283-7. OCLC 877846199. The bias generated by this sort of measurement error in regressors is called attenuation bias.

Наука и эксперименты

Когда либо случайность или неопределенность, смоделированная теория вероятности связано с такими ошибками, они являются «ошибками» в том смысле, в котором этот термин используется в статистика; видеть ошибки и остатки в статистике.

Каждый раз, когда мы повторяем измерение чувствительным прибором, мы получаем несколько разные результаты. Общее статистическая модель Используется в том, что ошибка состоит из двух дополнительных частей:

Систематическая ошибка что всегда происходит с одним и тем же значением, когда мы используем инструмент одинаково и в одном и том же случае
Случайная ошибка которые могут отличаться от наблюдения к другому.

Систематическая ошибка иногда называется статистическая погрешность. Его часто можно уменьшить с помощью стандартных процедур. Часть учебного процесса в различных науки учится использовать стандартные инструменты и протоколы, чтобы минимизировать систематические ошибки.

Случайная ошибка (или случайное изменение ) происходит из-за факторов, которые нельзя или не будут контролировать. Возможная причина отказа от контроля этих случайных ошибок заключается в том, что контролировать их каждый раз, когда проводится эксперимент или измерения, может быть слишком дорого. Другие причины могут заключаться в том, что все, что мы пытаемся измерить, изменяется во времени (см. динамические модели ) или фундаментально вероятностный (как в случае с квантовой механикой — см. Измерение в квантовой механике ). Случайная ошибка часто возникает, когда инструменты работают на пределе своих рабочих пределов. Например, цифровые весы часто показывают случайную ошибку в младшем разряде. Три измерения одного объекта могут показывать что-то вроде 0,9111 г, 0,9110 г и 0,9112 г.

Случайные ошибки против систематических ошибок

Ошибки измерения можно разделить на две составляющие: случайная ошибка и систематическая ошибка.^[2]

Случайная ошибка всегда присутствует в измерении. Это вызвано непредсказуемыми по своей природе колебаниями в показаниях измерительного прибора или в интерпретации экспериментатором показаний прибора. Случайные ошибки проявляются как разные результаты якобы одного и того же повторного измерения. Их можно оценить путем сравнения нескольких измерений и уменьшить путем усреднения нескольких измерений.

Систематическая ошибка является предсказуемым и обычно постоянным или пропорциональным истинному значению. Если причину систематической ошибки можно определить, то обычно ее можно устранить. Систематические ошибки вызваны несовершенной калибровкой средств измерений или несовершенными методами измерения. наблюдение или вмешательство среда с процессом измерения и всегда влияют на результаты эксперимент в предсказуемом направлении. Неправильная установка нуля прибора, приводящая к ошибке нуля, является примером систематической ошибки прибора.

Стандарт испытаний производительности PTC 19.1-2005 «Неопределенность испытаний», опубликованный Американским обществом инженеров-механиков (ASME), детально описывает систематические и случайные ошибки. Фактически, он концептуализирует свои основные категории неопределенности в этих терминах. Случайная ошибка может быть вызвана непредсказуемыми флуктуациями в показаниях измерительного прибора или в интерпретации экспериментатором показаний прибора; эти колебания могут быть частично вызваны вмешательством окружающей среды в процесс измерения. Концепция случайной ошибки тесно связана с концепцией точность. Чем выше точность измерительного прибора, тем меньше вариабельность (стандартное отклонение ) колебаний его показаний.

Источники систематической ошибки

Несовершенная калибровка

Источниками систематической погрешности могут быть несовершенная калибровка средств измерений (погрешность нуля), изменение среда которые мешают процессу измерения и иногда несовершенные методы наблюдение может быть либо нулевой ошибкой, либо процентной ошибкой. Если вы представите экспериментатора, который измеряет период времени маятника, который проходит мимо реперный маркер: Если их секундомер или таймер запускаются с 1 секундой на часах, то все их результаты будут отключены на 1 секунду (нулевая ошибка). Если экспериментатор повторит этот эксперимент двадцать раз (начиная с 1 секунды каждый раз), то будет процентная ошибка в рассчитанном среднем их результатах; конечный результат будет немного больше истинного периода.

Расстояние измеряется радар будет систематически переоцениваться, если не учитывать небольшое замедление волн в воздухе. Неправильная установка нуля прибора, приводящая к ошибке нуля, является примером систематической ошибки прибора.

Систематические ошибки также могут присутствовать в результате оценивать на основе математическая модель или же физический закон. Например, оценочная частота колебаний из маятник будет систематически ошибаться, если не учтено небольшое движение поддержки.

Количество

Систематические ошибки могут быть постоянными или связаны (например, пропорциональными или процентными) с фактическим значением измеренной величины или даже со значением другой величины (показание линейка может зависеть от температуры окружающей среды). Если он постоянный, это просто из-за неправильного обнуления прибора. Когда он непостоянен, он может менять знак. Например, если на термометр действует пропорциональная систематическая ошибка, равная 2% от фактической температуры, а фактическая температура составляет 200 °, 0 ° или −100 °, измеренная температура будет 204 ° (систематическая ошибка = + 4 °), 0 ° (нулевая систематическая ошибка) или −102 ° (систематическая ошибка = −2 °) соответственно. Таким образом, температура будет завышена, когда она будет выше нуля, и занижена, когда она будет ниже нуля.

Дрейф

Систематические ошибки, изменяющиеся в процессе эксперимента (дрейф ) легче обнаружить. Измерения указывают на тенденции во времени, а не на случайные колебания иметь в виду. Дрейф очевиден, если измерение постоянный количество повторяется несколько раз, и во время эксперимента измерения смещаются в одну сторону. Если следующее измерение выше, чем предыдущее, что может произойти, если прибор нагревается во время эксперимента, тогда измеряемая величина является переменной, и можно обнаружить дрейф, проверяя нулевое показание во время эксперимента, а также в начале эксперимент (действительно, нулевое показание является мерой постоянной величины). Если нулевое показание постоянно выше или ниже нуля, имеется систематическая ошибка. Если это не может быть устранено, потенциально путем сброса прибора непосредственно перед экспериментом, тогда это необходимо разрешить, вычтя его (возможно, изменяющееся во времени) значение из показаний и приняв его во внимание при оценке точности измерения.

Если закономерностей в серии повторных измерений не наблюдается, наличие фиксированных систематических ошибок может быть обнаружено только в том случае, если измерения проверены либо путем измерения известной величины, либо путем сравнения показаний с показаниями, полученными с помощью другого устройства, известного как более точным. Например, если вы думаете о времени маятника, используя точный секундомер несколько раз вам будут представлены значения, распределенные случайным образом относительно среднего значения. Систематическая ошибка Hopings присутствует, если секундомер сравнивается с ‘говорящие часы ‘телефонной системы и оказалось, что она работает медленно или быстро. Очевидно, что время маятника необходимо корректировать в соответствии с тем, насколько быстро или медленно работает секундомер.

Измерительные инструменты, такие как амперметры и вольтметры необходимо периодически проверять соответствие известным стандартам.

Систематические ошибки также можно обнаружить путем измерения уже известных величин. Например, спектрометр оснащен дифракционная решетка можно проверить, используя его для измерения длина волны D-линий натрий электромагнитный спектр которые находятся на 600 нм и 589,6 нм. Измерения могут использоваться для определения количества линий на миллиметр дифракционной решетки, которые затем могут использоваться для измерения длины волны любой другой спектральной линии.

Постоянные систематические ошибки очень трудно устранить, поскольку их влияние можно наблюдать только в том случае, если их можно устранить. Такие ошибки невозможно устранить повторением измерений или усреднением большого количества результатов. Распространенный метод устранения систематической ошибки — это калибровка измерительного прибора.

Источники случайной ошибки

Случайная или стохастическая ошибка в измерении — это ошибка, которая является случайной от одного измерения к другому. Стохастические ошибки обычно нормально распределенный когда стохастическая ошибка является суммой многих независимых случайных ошибок из-за Центральная предельная теорема. Стохастические ошибки, добавленные в уравнение регрессии, учитывают изменение Y что не может быть объяснено включенным Иксс.

Обзоры

Термин «ошибка наблюдения» также иногда используется для обозначения ошибок ответа и некоторых других типов ошибка, не связанная с выборкой.^[1] В ситуациях типа опроса эти ошибки могут быть ошибками при сборе данных, включая как неправильную запись ответа, так и правильную запись неточного ответа респондента. Эти источники ошибок, не связанных с выборкой, обсуждаются у Саланта и Диллмана (1994) и Бланда и Альтмана (1996).^[4]^[5]

Эти ошибки могут быть случайными или систематическими. Случайные ошибки вызваны непреднамеренными ошибками респондентов, интервьюеров и / или кодировщиков. Систематическая ошибка может возникать при систематической реакции респондентов на метод, использованный при формулировке вопроса опроса. Таким образом, точная формулировка вопроса обследования имеет решающее значение, поскольку она влияет на уровень ошибки измерения.^[6] Исследователям доступны различные инструменты, которые помогут им решить эту точную формулировку вопросов, например, оценка качества вопроса с помощью MTMM эксперименты. Эта информация о качестве также может быть использована для исправить ошибку измерения.^[7]^[8]

Влияние на регрессионный анализ

Если зависимая переменная в регрессии измеряется с ошибкой, регрессионный анализ и соответствующая проверка гипотез не затрагиваются, за исключением того, что р² будет ниже, чем при идеальном измерении.

Однако, если один или несколько независимые переменные измеряется с ошибкой, то коэффициенты регрессии и стандартные проверка гипотез недействительны.^[9]^{:п. 187}

Смотрите также

Смещение (статистика)
Когнитивное искажение
Поправка на ошибку измерения (для корреляций Пирсона)
Ошибки и неточности в статистике
Ошибка
Репликация (статистика)
Статистическая теория
Метрология
Разбавление регрессии
Метод испытания
Распространение неопределенности
Ошибка прибора
Погрешность измерения
Модели с ошибками в переменных
Системная предвзятость

дальнейшее чтение

Кокран, У. Г. (1968). «Ошибки измерения в статистике». Технометрика. 10 (4): 637–666. Дои:10.2307/1267450. JSTOR 1267450.

Источник

Разница между случайной ошибкой и систематической ошибкой

Ошибка определяется как разница между фактическим или истинным значением и измеренным значением. Измерение количества или стоимости основано на каком-то стандарте. Измерение любого количества осуществляется путем сравнения его с производным стандартом, который не является полностью точным. Чтобы понять ошибки в измерении, следует понимать два термина, которые определяют ошибку, и они являются истинным значением и измеренным значением. Истинное значение невозможно выяснить, оно может быть определено по среднему значению бесконечного числа. Измеренное значение определяется как оценочное значение истинного значения путем взятия нескольких измеренных значений. Ошибка не должна быть перепутана с ошибкой, ошибки можно избежать, но ошибки не избежать, но их можно минимизировать. Так что ошибка не является ошибкой его части измерительной обработки. Измерение — это разница между измеренным значением количества и его истинным значением. мы обсудим случайную ошибку и систематическую ошибку. Погрешности измерения делятся на два обширных класса ошибок.

Случайная ошибка
Систематическая ошибка

Случайная ошибка:

Случайная ошибка — это не что иное, как колебания в измерении, которые в основном наблюдаются путем проведения нескольких испытаний данного измерения. Как следует из названия, эта ошибка происходит совершенно случайно. Они непредсказуемы и не могут быть воспроизведены путем повторения эксперимента снова. Так что каждый раз это дает разные результаты. Случайная ошибка варьируется от наблюдения к другому. При случайной ошибке колебание может быть как отрицательным, так и положительным. Не всегда возможно определить источник случайной ошибки. Случайная ошибка происходит из-за фактора, который не может или не будет контролироваться. Случайная ошибка влияет на достоверность результатов. Некоторые из возможных источников или причин случайных ошибок перечислены ниже.

Наблюдение: ошибка в суждении наблюдателя.
Небольшие помехи: Небольшие помехи могут привести к ошибкам измерения, например
Колеблющиеся условия: Некоторое изменение температуры во времени или в окружающей среде может привести к ошибке в измерении.
Качество: Некоторое время, когда качество объекта, измерение которого должно быть выполнено, не определено должным образом, приводит к ошибке.

Ошибка может быть уменьшена, если взять число чтений, а затем найти среднее или среднее значение чтения.

Систематическая ошибка:

Систематическая ошибка — это когда одна и та же ошибка присутствует во всех показаниях. Систематическая ошибка предсказуема и обычно постоянна или пропорциональна истинному значению. Таким образом, систематическая ошибка повторяется каждый раз, и это приводит к ошибкам согласованности. Если мы повторим эксперимент, мы получим одну и ту же ошибку каждый раз. Систематические ошибки возникают из-за неправильной калибровки прибора. Систематическая ошибка влияет на точность результата. Систематическая ошибка также называется нулевой ошибкой, положительной или отрицательной ошибкой. Некоторые из возможных источников или причин систематической ошибки перечислены ниже.

Инструментальная ошибка: оборудование, используемое для измерения объекта, может быть не совсем точным.
Экологическая ошибка: ошибка возникает из-за изменений условий окружающей среды, таких как влажность, давление, температура и т. Д.
Наблюдательная ошибка: ошибка в записи данных, также называемая человеческими ошибками. После выявления систематической ошибки она может быть в некоторой степени уменьшена. Систематическая ошибка может быть сведена к минимуму путем регулярной калибровки оборудования, использования элементов управления и сравнения значений со стандартным значением.

Сравнение между случайными ошибками и значением систематической ошибки (инфографика)

Ниже приведено 8 основных различий между случайной ошибкой и систематической ошибкой

Ключевые различия между случайной ошибкой и систематической ошибкой

Давайте обсудим некоторые основные различия между случайной ошибкой и систематической ошибкой

Случайная ошибка непредсказуема и возникает из-за неизвестных источников, тогда как систематическая ошибка является предсказуемой и возникает из-за дефекта прибора, который используется для измерения.
Случайная ошибка возникает в обоих направлениях, тогда как систематическая ошибка возникает только в одном направлении.
Случайная ошибка не может быть устранена, но большинство систематических ошибок может быть уменьшено.
Случайная ошибка является уникальной и не имеет определенного типа, тогда как систематическая ошибка имеет 3 типа, как указано в таблице выше.
Систематическую ошибку трудно обнаружить, это происходит из-за одних и тех же результатов каждый раз и не осознает, что проблема вообще существует, тогда как случайную ошибку легко обнаружить из-за разных результатов каждый раз.

Сравнительная таблица случайных ошибок и систематических ошибок

Ниже приведено 8 лучших сравнений между случайной ошибкой и систематической ошибкой.

Основное сравнение между случайной ошибкой и систематической ошибкой	Случайная ошибка	Систематическая ошибка
Определение	Это происходит из-за неопределенных изменений в окружающей среде и колеблется каждый раз при измерении.	Это постоянная ошибка и остается неизменной для всех измерений.
Свести к минимуму	Путем многократного взятия показаний и расчета среднего или среднего из повторных показаний.	Сравнивая значение со стандартным значением и улучшая структуру оборудования.
Величина ошибки	Каждый раз дают другой результат, который меняется каждый раз.	Результат остается неизменным или постоянным каждый раз.
Направление ошибки	Это происходит в обоих направлениях.	Это происходит в том же направлении.
Подтип ошибки	Нет подтипов	Подтипы Инструмент, Среда и Систематическая Ошибка.
воспроизводимый	Невоспроизводимый.	Воспроизводимые.
Значение	Цена представляет собой сочетание стоимости.	Затраты снижаются, когда они сравниваются со стоимостью в стоимостном выражении.
Пример ошибки	Время реакции, погрешность измерения из-за недостаточной точности, погрешность параллакса (если каждый раз смотреть под случайным углом)	Ошибка шкалы, ошибка нуля, ошибка параллакса (если диск виден под тем же углом)

Выводы

Таким образом, случайная ошибка в основном возникает из-за каких-либо возмущений в окружающей среде, таких как колебания или различия в давлении, температуре или из-за наблюдателя, который может принять неправильные показания, в то время как систематическая ошибка возникает из-за механической структуры прибора. Случайная ошибка не может быть предотвращена, в то время как систематическая ошибка может быть предотвращена. Полное устранение обеих ошибок невозможно. Основное различие между случайными ошибками и систематическими ошибками заключается в том, что случайная ошибка в основном приводит к колебаниям, тогда как систематические ошибки приводят к предсказуемому и последовательному результату. При работе с промышленными приборами важно, чтобы оператор тщательно следил за экспериментом, чтобы погрешность измерения могла быть уменьшена.

Что может быть причиной случайной ошибки измерения

3.4 Грубые погрешности и промахи. Статические и динамические погрешности

1.1 Результат измерения

О необходимости оценки погрешностей.

1.2 Многократные измерения

1.3 Классификация погрешностей

1.3.1 Случайные погрешности

1.3.2 Систематические погрешности

Science and experiments[edit]

Characterization[edit]

Sources[edit]

Sources of systematic error[edit]

Imperfect calibration[edit]

Quantity[edit]

Drift[edit]

Sources of random error[edit]

Surveys[edit]

Effect on regression analysis[edit]

See also[edit]

References[edit]

Further reading[edit]

Science and experiments[edit]

Characterization[edit]

Sources[edit]

Sources of systematic error[edit]

Imperfect calibration[edit]

Quantity[edit]

Drift[edit]

Sources of random error[edit]

Surveys[edit]

Effect on regression analysis[edit]

See also[edit]

References[edit]

Further reading[edit]

Наука и эксперименты

Случайные ошибки против систематических ошибок

Источники систематической ошибки

Несовершенная калибровка

Количество

Дрейф

Источники случайной ошибки

Обзоры

Влияние на регрессионный анализ

Смотрите также

Рекомендации

дальнейшее чтение

Разница между случайной ошибкой и систематической ошибкой

Случайная ошибка:

Систематическая ошибка:

Сравнение между случайными ошибками и значением систематической ошибки (инфографика)

Ключевые различия между случайной ошибкой и систематической ошибкой

Сравнительная таблица случайных ошибок и систематических ошибок

Выводы

Рекомендуемые статьи

А вот еще интересные материалы: