Загрузить PDF
Загрузить PDF
Стандартной ошибкой называется величина, которая характеризует стандартное (среднеквадратическое) отклонение выборочного среднего. Другими словами, эту величину можно использовать для оценки точности выборочного среднего. Множество областей применения стандартной ошибки по умолчанию предполагают нормальное распределение. Если вам нужно рассчитать стандартную ошибку, перейдите к шагу 1.
-

1
Запомните определение среднеквадратического отклонения. Среднеквадратическое отклонение выборки – это мера рассеянности значения. Среднеквадратическое отклонение выборки обычно обозначается буквой s. Математическая формула среднеквадратического отклонения приведена выше.
-

2
Узнайте, что такое истинное среднее значение. Истинное среднее является средним группы чисел, включающим все числа всей группы – другими словами, это среднее всей группы чисел, а не выборки.
-

3
Научитесь рассчитывать среднеарифметическое значение. Среднеаримфетическое означает попросту среднее: сумму значений собранных данных, разделенную на количество значений этих данных.
-

4
Узнайте, что такое выборочное среднее. Когда среднеарифметическое значение основано на серии наблюдений, полученных в результате выборок из статистической совокупности, оно называется “выборочным средним”. Это среднее выборки чисел, которое описывает среднее значение лишь части чисел из всей группы. Его обозначают как:
-

5
Усвойте понятие нормального распределения. Нормальные распределения, которые используются чаще других распределений, являются симметричными, с единичным максимумом в центре – на среднем значении данных. Форма кривой подобна очертаниям колокола, при этом график равномерно опускается по обе стороны от среднего. Пятьдесят процентов распределения лежит слева от среднего, а другие пятьдесят процентов – справа от него. Рассеянность значений нормального распределения описывается стандартным отклонением.
-

6
Запомните основную формулу. Формула для вычисления стандартной ошибки приведена выше.
Реклама
-

1
Рассчитайте выборочное среднее. Чтобы найти стандартную ошибку, сначала нужно определить среднеквадратическое отклонение (поскольку среднеквадратическое отклонение s входит в формулу для вычисления стандартной ошибки). Начните с нахождения средних значений. Выборочное среднее выражается как среднее арифметическое измерений x1, x2, . . . , xn. Его рассчитывают по формуле, приведенной выше.
- Допустим, например, что вам нужно рассчитать стандартную ошибку выборочного среднего результатов измерения массы пяти монет, указанных в таблице:
Вы сможете рассчитать выборочное среднее, подставив значения массы в формулу:
- Допустим, например, что вам нужно рассчитать стандартную ошибку выборочного среднего результатов измерения массы пяти монет, указанных в таблице:
-

2
Вычтите выборочное среднее из каждого измерения и возведите полученное значение в квадрат. Как только вы получите выборочное среднее, вы можете расширить вашу таблицу, вычтя его из каждого измерения и возведя результат в квадрат.
- Для нашего примера расширенная таблица будет иметь следующий вид:
-

3
Найдите суммарное отклонение ваших измерений от выборочного среднего. Общее отклонение – это сумма возведенных в квадрат разностей от выборочного среднего. Чтобы определить его, сложите ваши новые значения.
- В нашем примере нужно будет выполнить следующий расчет:
Это уравнение дает сумму квадратов отклонений измерений от выборочного среднего.
- В нашем примере нужно будет выполнить следующий расчет:
-

4
Рассчитайте среднеквадратическое отклонение ваших измерений от выборочного среднего. Как только вы будете знать суммарное отклонение, вы сможете найти среднее отклонение, разделив ответ на n -1. Обратите внимание, что n равно числу измерений.
- В нашем примере было сделано 5 измерений, следовательно n – 1 будет равно 4. Расчет нужно вести следующим образом:
-

5
Найдите среднеквадратичное отклонение. Сейчас у вас есть все необходимые значения для того, чтобы воспользоваться формулой для нахождения среднеквадратичного отклонения s.
- В нашем примере вы будете рассчитывать среднеквадратичное отклонение следующим образом:
Следовательно, среднеквадратичное отклонение равно 0,0071624.
Реклама
- В нашем примере вы будете рассчитывать среднеквадратичное отклонение следующим образом:
-

1
Чтобы вычислить стандартную ошибку, воспользуйтесь базовой формулой со среднеквадратическим отклонением.
- В нашем примере вы сможете рассчитать стандартную ошибку следующим образом:
Таким образом в нашем примере стандартная ошибка (среднеквадратическое отклонение выборочного среднего) составляет 0,0032031 грамма.
- В нашем примере вы сможете рассчитать стандартную ошибку следующим образом:
Советы
- Стандартную ошибку и среднеквадратическое отклонение часто путают. Обратите внимание, что стандартная ошибка описывает среднеквадратическое отклонение выборочного распределения статистических данных, а не распределения отдельных значений
- В научных журналах понятия стандартной ошибки и среднеквадратического отклонения несколько размыты. Для объединения двух величин используется знак ±.
Реклама
Об этой статье
Эту страницу просматривали 48 054 раза.
Была ли эта статья полезной?
Чтобы
судить о том, насколько точно проведенные
измерения отражают состав генеральной
совокупности, необходимо вычислить
стандартную ошибку средней арифметической
выборочной совокупности.
Стандартная
ошибка средней арифметической
характеризует степень отклонения
выборочной средней арифметической от
средней арифметической генеральной
совокупности.
Стандартная
ошибка средней арифметической вычисляется
по формуле:
![]() ,
,
где
– стандартное отклонение результатов
измерений, n
– объем выборки.
Зачастую
мы имеем дело с одной случайной выборкой
и с одной полученной при ее обработке
выборочной средней. Задача заключается
в суждении о величине неизвестной
генеральной средней по полученной
неточной величине случайной выборочной
средней.
Вычислим
среднюю ошибку найденного выборочного
среднего значения роста:
![]() 195
195
см; σ = 8,8 см;
![]() см.
см.
2,8 см
составляют не максимальную, а среднюю
возможную ошибку среднего. Отдельные
выборочные средние могут отклоняться
от генеральной как больше, так и меньше,
чем на 2,8 см.
Каковы
же пределы возможных ошибок случайной
выборки, какова ее максимальная ошибка?
Величина максимальной ошибки зависит
от величины средней ошибки и вычисляется
по формуле
![]() .
.
При
объеме выборки n
= 10:
![]() .
.
Все
случайные выборочные средние, которые
могут быть получены в подобных опытах
(в том числе и фактически полученная
выборочная средняя
![]() = 195 см), при своем варьировании около
= 195 см), при своем варьировании около
неизвестного генерального среднего в
подавляющем количестве группируются
около него так, что лишь ничтожный
процент их отклоняется от генеральной
средней более, чем на величину максимальной
ошибки.
Другими
словами, генеральная средняя определяется
как
![]() .
.
Эти пределы
колебаний значительно сужаются, если
средняя ошибка уменьшается благодаря
увеличению численности выборки.
Искомая
генеральная средняя лежит между
![]() и
и![]() .
.
Таким образом, при высокой точности
выполнения эксперимента и достаточно
большом числе измерений можно определить
среднюю арифметическую бесконечно
большого числа экспериментов.
До сих
пор мы определяли максимальную ошибку
выборочной средней, исходя из того, что
все остальные показатели известны. Если
же мы хотим достичь определенной
точности, определенного приближения к
генеральной средней, в этом случае
встает вопрос о численности выборки (о
том, сколько измерений, опытов необходимо
провести).
Допустим, что
максимальная ошибка должна быть равна
5 см. Сколько человек надо обследовать
(измерить) в нашем случае?
![]() .
.
Следовательно,
мы должны провести измерения роста у
36 баскетболистов высокого класса.
10. Достоверность различий
Следующим
важным вопросом практически для каждого
экспериментатора является умение
доказать достоверность различий между
двумя рядами признаков.
Проверку
достоверности различия двух рядов
измерений производят путем вычисления
критерия достоверности различия – t:
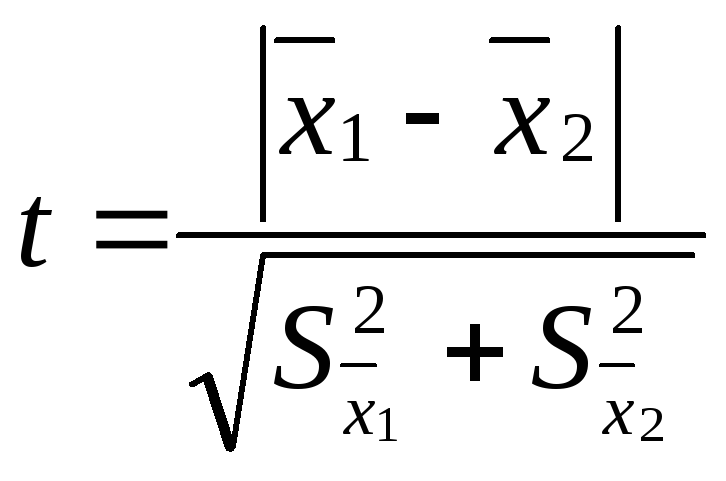 ,
,
где
![]() – средняя одной выборки;
– средняя одной выборки;![]() – средняя другой выборки;
– средняя другой выборки;![]() – средняя ошибка первой выборки;
– средняя ошибка первой выборки;![]() – второй выборки. Если t < 2, то различие
– второй выборки. Если t < 2, то различие
между двумя выборками считается
недостоверным, если t
2, то различие между двумя выборками
достоверно на 95%.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Стандартное отклонение и стандартная ошибка: в чем разница?
17 авг. 2022 г.
читать 2 мин
В статистике студенты часто путают два термина: стандартное отклонение и стандартная ошибка .
Стандартное отклонение измеряет, насколько разбросаны значения в наборе данных.
Стандартная ошибка — это стандартное отклонение среднего значения в повторных выборках из совокупности.
Давайте рассмотрим пример, чтобы ясно проиллюстрировать эту идею.
Пример: стандартное отклонение против стандартной ошибки
Предположим, мы измеряем вес 10 разных черепах.
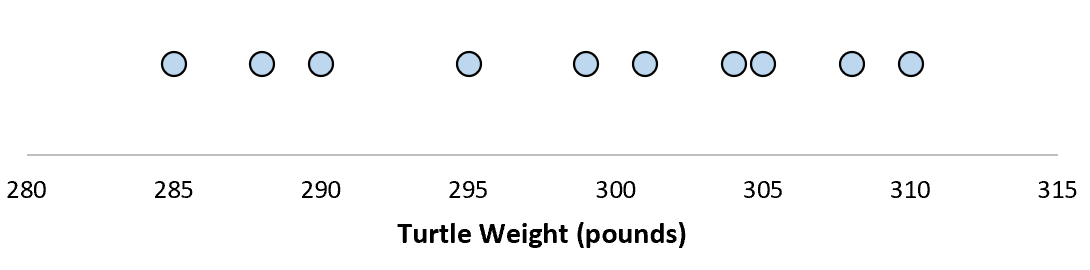
Для этой выборки из 10 черепах мы можем вычислить среднее значение выборки и стандартное отклонение выборки:
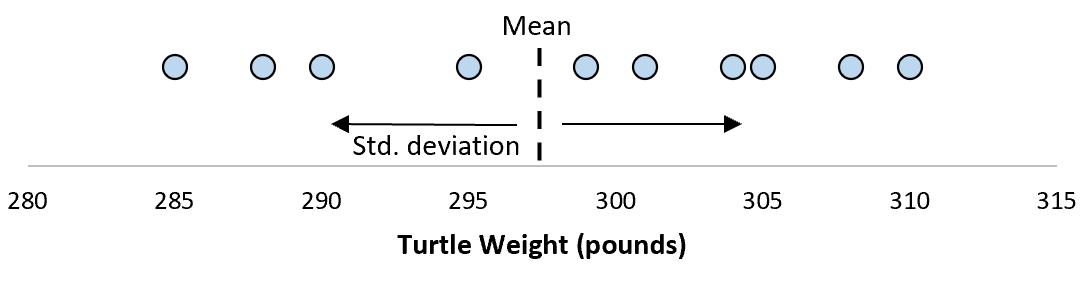
Предположим, что стандартное отклонение оказалось равным 8,68. Это дает нам представление о том, насколько распределен вес этих черепах.
Но предположим, что мы собираем еще одну простую случайную выборку из 10 черепах и также проводим их измерения. Более чем вероятно, что эта выборка из 10 черепах будет иметь немного другое среднее значение и стандартное отклонение, даже если они взяты из одной и той же популяции:
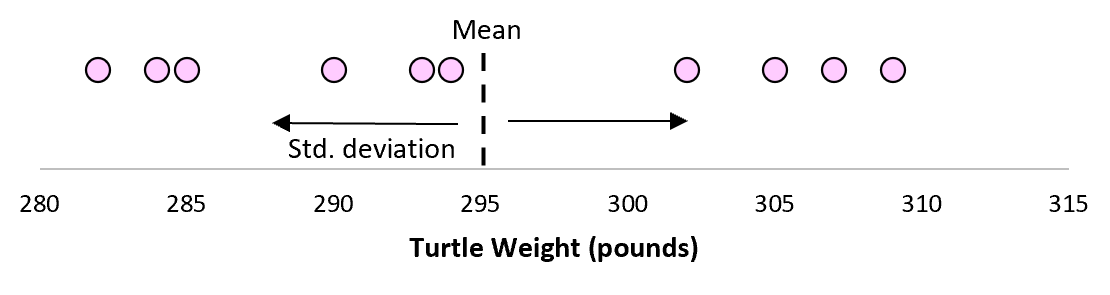
Теперь, если мы представим, что мы берем повторные выборки из одной и той же совокупности и записываем выборочное среднее и выборочное стандартное отклонение для каждой выборки:
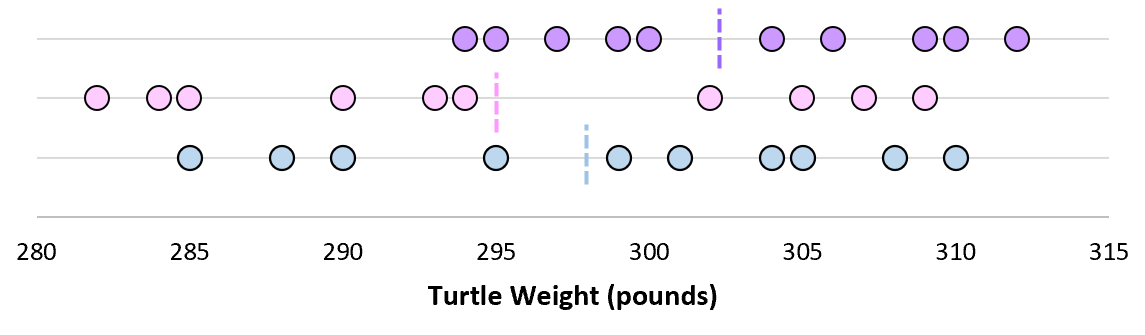
Теперь представьте, что мы наносим каждое среднее значение выборки на одну и ту же строку:
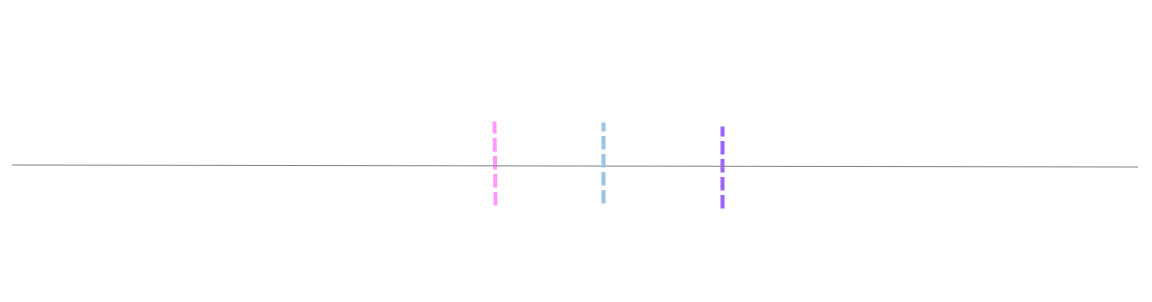
Стандартное отклонение этих средних значений известно как стандартная ошибка.
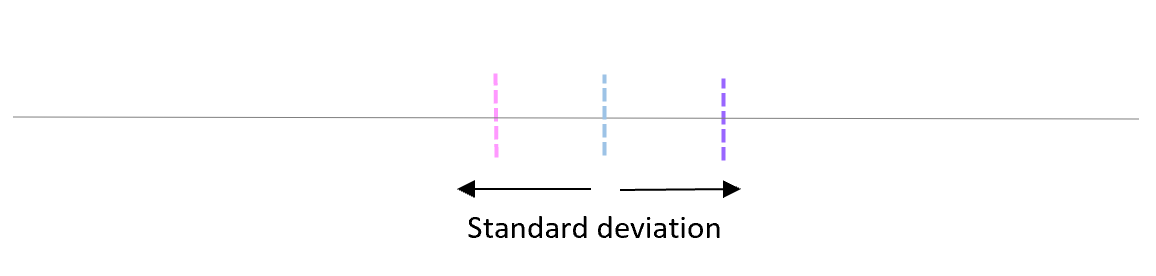
Формула для фактического расчета стандартной ошибки:
Стандартная ошибка = s/ √n
куда:
- s: стандартное отклонение выборки
- n: размер выборки
Какой смысл использовать стандартную ошибку?
Когда мы вычисляем среднее значение данной выборки, нас на самом деле интересует не среднее значение этой конкретной выборки, а скорее среднее значение большей совокупности, из которой взята выборка.
Однако мы используем выборки, потому что для них гораздо проще собирать данные, чем для всего населения. И, конечно же, среднее значение выборки будет варьироваться от выборки к выборке, поэтому мы используем стандартную ошибку среднего значения как способ измерить, насколько точна наша оценка среднего значения.
Вы заметите из формулы для расчета стандартной ошибки, что по мере увеличения размера выборки (n) стандартная ошибка уменьшается:
Стандартная ошибка = s/ √n
Это должно иметь смысл, поскольку большие размеры выборки уменьшают изменчивость и увеличивают вероятность того, что среднее значение нашей выборки ближе к фактическому среднему значению генеральной совокупности.
Когда использовать стандартное отклонение против стандартной ошибки
Если мы просто заинтересованы в измерении того, насколько разбросаны значения в наборе данных, мы можем использовать стандартное отклонение .
Однако, если мы заинтересованы в количественной оценке неопределенности оценки среднего значения, мы можем использовать стандартную ошибку среднего значения .
В зависимости от вашего конкретного сценария и того, чего вы пытаетесь достичь, вы можете использовать либо стандартное отклонение, либо стандартную ошибку.
СТАНДАРТНАЯ ОШИБКА
- СТАНДАРТНАЯ ОШИБКА
- — величина, характеризующая случайную ошибку выборки — стандартное отклонение выборочного распределения статистики; обозначается SE (standard error). Может вычисляться для любых выборочных статистик; используется при построении соответствующих доверительных интервалов и статистической проверке гипотез .
Наиболее часто используется С.О. среднего арифметического . Она вычисляется по формуле SE = s / Vn, где s — стандартное отклонение переменной, n — объем выборки. Чем меньше стандартное отклонение s и больше объем выборки n, тем меньше С.О. С.О. среднего арифметического применяется при построении доверительного интервала для математического ожидания , интервального оценивания случайной ошибки выборки , нахождения объема репрезентативной выборки при заданных доверительной вероятности и предельно допустимой ошибке выборки.
О.В. Терещенко
Социология: Энциклопедия. — Минск: Интерпрессервис; Книжный Дом.
.
2003.
Смотреть что такое «СТАНДАРТНАЯ ОШИБКА» в других словарях:
-
СТАНДАРТНАЯ ОШИБКА — (standard error) Показатель надежности расчетного параметра. Стандартная ошибка – это стандартное отклонение оценок, которые будут получены при многократной случайной выборке данного размера из одной и той же совокупности. Стандартная ошибка –… … Экономический словарь
-
Стандартная ошибка — * стандартная памылка * standard error or SE мера изменчивости (см.) среднепопуляционных значений. SE = s / N?1, где N число особей (измерений) в популяции (в выборке), s стандартное отклонение (см.) … Генетика. Энциклопедический словарь
-
СТАНДАРТНАЯ ОШИБКА — см. ВЫБОРКИ ОШИБКА. Antinazi. Энциклопедия социологии, 2009 … Энциклопедия социологии
-
стандартная ошибка — 2.56. стандартная ошибка; среднеквадратичная ошибка Стандартное отклонение оценки Источник: ГОСТ Р 50779.10 2000: Статистические методы. Вероятность и основы статистики. Термины и определения … Словарь-справочник терминов нормативно-технической документации
-
СТАНДАРТНАЯ ОШИБКА — Стандартное отклонение распределения теоретической выборки. Оно обеспечивает оценку вариативности, которая может ожидаться в фактических выборках из основной теоретической популяции и, таким образом, и в популяционном параметре. См. стандартная… … Толковый словарь по психологии
-
стандартная ошибка — Стандартное отклонение статистики, в частности, выборочного распределения оценки. Как правило, употребляется в выражениях типа «стандартная ошибка среднего» (которая равна стандартному отклонению, деленному на корень квадратный из… … Словарь социологической статистики
-
СТАНДАРТНАЯ ОШИБКА ВЫБОРКИ — см. ВЫБОРКИ ОШИБКА. Antinazi. Энциклопедия социологии, 2009 … Энциклопедия социологии
-
СТАНДАРТНАЯ ОШИБКА — (standard error) см. Меры дисперсии … Большой толковый социологический словарь
-
СТАНДАРТНАЯ ОШИБКА ИЗМЕРЕНИЯ — Оценка степени, в которой можно ожидать, что определенный набор измерений, полученных в данной ситуации (например, в тесте или в одной из нескольких параллельных форм теста), будет отклоняться от истинных значений. Обозначается как а (М) … Толковый словарь по психологии
-
СТАНДАРТНАЯ ОШИБКА ОЦЕНКИ — Оценка степени ошибки, вероятность возникновения которой имеется, когда используется уравнение регрессии для предсказания (или оценка) значений одной переменной на основании значений другой, коррелирующей с ней, переменной. Она вычисляется по… … Толковый словарь по психологии
Я читаю курс статистического мышления магистрам, и одна тема вызывает у них явные затруднения – чем стандартное отклонение отличается от стандартной ошибки, и в каких случаях, применять ту или иную статистику. А недавно в книге Искусство статистики Дэвида Шпигельхалтера я узнал про бутстрэппинг, и понял, как объяснить различия стандартного отклонения и стандартной ошибки.
Для начала зададим 100 значений стандартной нормально распределенной случайной величины. В этом контексте стандартная означает, что ее матожидание μ = 0, а среднеквадратичное отклонение σ = 1. Поскольку значения в Excel получены с помощью волатильной функции СЛМАССИВ(), после любого действия они пересчитываются. Поэтому диаграммы в заметке и в файле будут отличаться.
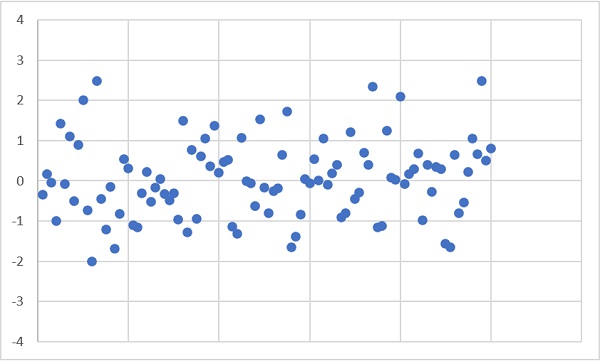
Рис. 1. Нормально распределенная случайная величина
Скачать заметку в формате Word или pdf, примеры в формате Excel
Стандартное отклонение
… является наиболее распространенным показателем рассеивания значений случайной величины относительно её среднего арифметического.
Стандартное отклонение вычисляют по формуле:
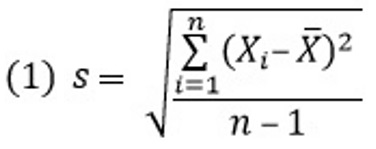
где X̅ – среднее арифметическое значений случайной величины (далее я буду называть его просто средним), Хi – отдельные значения случайной величины, n – число значений случайной величины.
Вообще термины разными авторами используются немного по-разному. Мне нравится следующий подход. Генеральную совокупность описывают параметрами, обозначаемыми греческими буквами: математическое ожидание μ и среднеквадратичное отклонение σ. Выборки описывают статистиками, обозначаемыми латинскими буквами: среднее арифметическое X̅ и стандартное отклонение s. Стандартное отклонение иначе называют оценкой среднеквадратичного отклонения. Как правило, есть генеральная совокупность с неизвестным нам среднеквадратичным отклонением σ. Извлекая выборку, и вычисляя стандартное отклонение s, мы кое-что узнаем о среднеквадратичном отклонении генеральной совокупности σ. Поэтому и говорят, что s является оценкой сигмы.
На самом деле за термином стандартное отклонение стоят две немного отличающиеся статистики. Но эта заметка о другом)) Подробнее см. СТАНДОТКЛОН.В и СТАНДОТКЛОН.Г: в чем различие?
Нанесем на диаграмму линию среднего и границы, отстоящие от среднего на расстоянии ±2s.

Рис. 2. Линия среднего и границы ±2s
Для стандартного нормального распределения за границы ±2s попадают 4,6% значений.
=(1-НОРМ.СТ.РАСП(2;ИСТИНА))*2 = 4,6%
И действительно 5 точек на рис. 2 лежат вне границ. Совпадение не обязано быть таким точным. Если вы откроете файл Excel на листе «Рис. 2» и понажимаете F9, принудительно изменяя случайные значения, то увидите, что вне границ может лежать от 2 до 8 точек. А если нажимать F9 достаточно долго, то вы получите более экстремальные числа точек вне границ. Для стандартного нормального распределения в пределах ±2s лежат приблизительно 95% значений. Поскольку s – оценка среднеквадратичного отклонения σ, которое в свою очередь равно 1, то 95% всех значений попадают в диапазон ≈ ±2.
Чем меньше s, тем кучнее значения случайной величины располагаются вокруг среднего. Итак
стандартное отклонение – мера разброса случайной величины
Среднее арифметическое выборки
Напомню, что мы задаем наши 100 значений с помощью генератора случайных чисел формулой в Excel
=НОРМ.СТ.ОБР(СЛМАССИВ(100;;0;1;ЛОЖЬ))
Хотя мы установили для генератора случайных чисел μ = 0 и σ = 1, значения X̅ и s будут немного отличаться для каждой выборки.
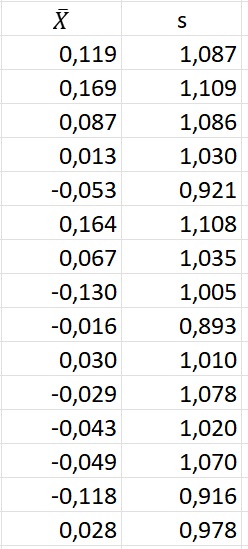
Рис. 3. Среднее и стандартное отклонение для 15 выборок размером n = 100
Теперь мы хотим узнать, что можно сказать о неизвестном математическом ожидании генеральной совокупности μ, подсчитав среднее арифметическое конкретной выборки, например, первой X̅ = 0,119?
Бутстрэп
Как пишет Евгения Поникарова, переводчик книги Дэвида Шпигельхалтера «Искусство статистики», слово bootstraps означает ремешки в виде ушка, которые прикрепляются к верхней части обуви, чтобы ее было проще натягивать. В английском языке есть выражение To pull oneself over a fence by one’s bootstraps (буквально — перетащить себя через ограду за ушки своей обуви), которое означает «выпутаться из своих проблем самому». Еще можно вспомнить барона Мюнхгаузена, который вытащил себя за волосы из болота.
Бутстрэп – компьютерный метод исследования распределения статистик, основанный на многократной генерации выборок методом Монте-Карло на базе имеющейся одной выборки. Термин ввел в 1977 году Брэдли Эфрон.
Итак, возьмем одну выборку из 100 случайных чисел и зафиксируем значения. Это наша исходная выборка (столбец А на рис. 4). Её среднее X̅(100) = 0,121, а стандартное отклонение s(100) = 0,995. 95% значений попадают в диапазон ≈ 0,121 ± 1,990.
С помощью генератора случайных чисел будем формировать из исходной выборки бутстрэп-выборки разного размера. Хитрость заключается в том, что выбирать значения мы будем с возвращением. Т.е., все значения любой бутстрэп-выборки взяты из исходной, а вот уникальность значений будет потеряна. Например, выборка в столбце С содержит два значения 0,7394. Я подсветил их с помощью условного форматирования. Опять же, если вы откроете Excel-файл, то дублей может не быть, так как бутстрэп-выборка сформирована волатильной функцией СЛМАССИВ().
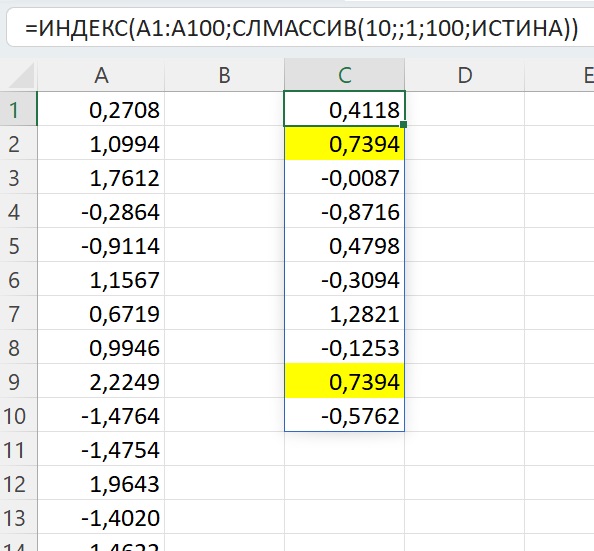
Рис. 4. Бутстрэп-выборка может содержать повторения
Для удобства последующей обработки расположим значения бутстрэп-выборки по горизонтали. Начнем со значения n = 3. Извлечем 1000 бутстрэп-выборок (рис. 5). В столбце А исходная выборка, n = 100. Столбец С содержит номер бутстрэп-выборки. В столбцах D, E и F извлеченные значения, в G – средние значения по выборкам. В ячейке G1 среднее D1:F1, в ячейке G2 – среднее D2:F2 и т.д. На диаграмме показано распределение средних значений бутстрэп-выборок для n = 3.
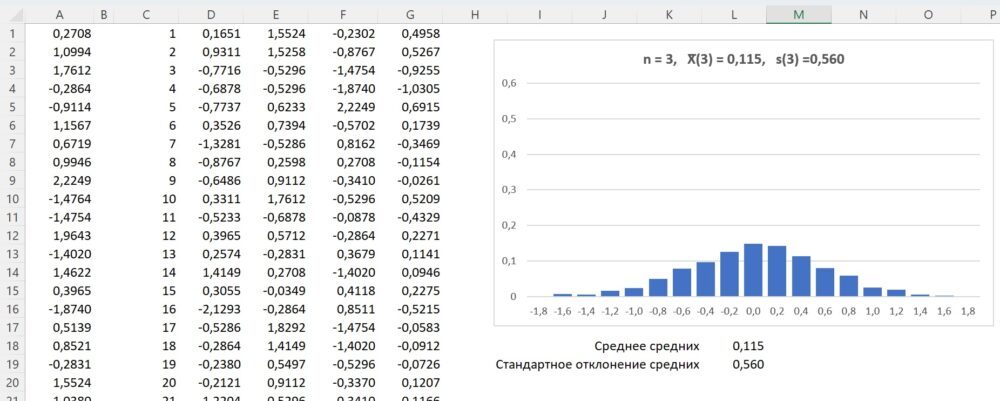
Рис. 5. Распределений средних значений 1000 бутстрэп-выборок, n = 3
Среднее средних 1000 бутстрэп-выборок = 0,115, стандартное отклонение средних значений 1000 бутстрэп-выборок = 0,560. Напоминаю, что 95% исходных значений выборки попадают в диапазон 0,12 ± 1,99. Для бутстрэп-выборок n = 3 мы только что нашли, что 95% средних попадают в диапазон 0,115 ± 1,120 (0,560*2 = 1,120). Кажется естественным, что разброс средних меньше, чем разброс отдельных значений.
Повторим моделирование для n = 5, 20, 50.
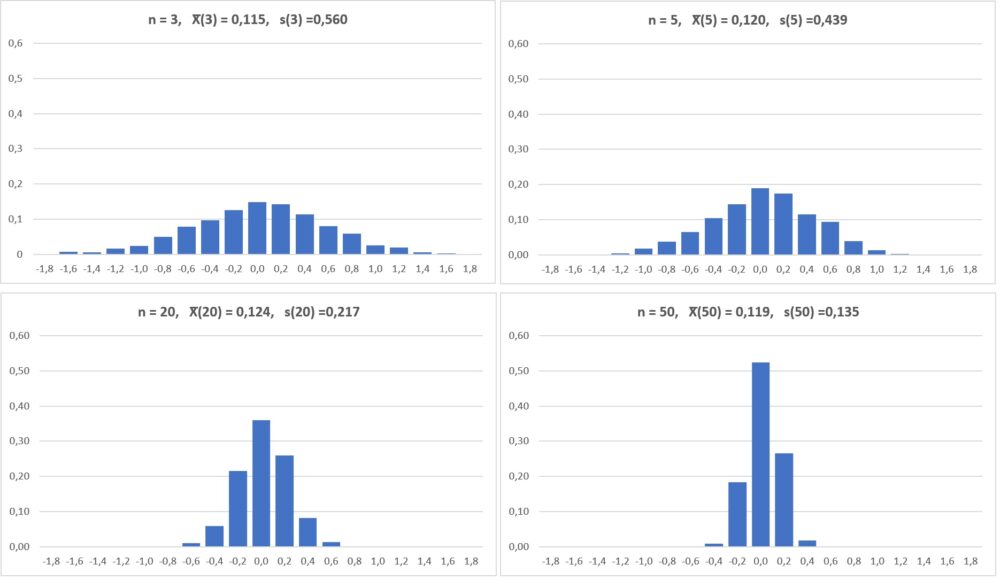
Рис. 6. С увеличением n стандартное отклонение средних значений бутстрэп-выборок уменьшается
Осмыслим, что мы получили. На рис. 6 представлены распределения средних значений бутстрэп-выборок разного размера из исходной выборки 100 случайных нормально распределенных чисел. Среднее каждого распределения близко к нулю (в нашей конкретной выборке из 100 чисел это среднее равно 0,121). А вот стандартное отклонение s(n) уменьшается по мере роста размера бутстрэп-выборок: s(3) = 0,560, s(5) = 0,439, s(20) = 0,217, s(50) = 0,135.
Стандартна ошибка
…или стандартная ошибка среднего – статистика, характеризующая стандартное отклонение выборочного среднего, рассчитанное по выборке размера n из генеральной совокупности.
Ничего не напоминает!? А что за статистику s(n) мы рассчитали выше в бутстрэп-анализе!? Да, это было стандартное отклонение выборочного среднего X̅(n).
Величина стандартной ошибки зависит от дисперсии генеральной совокупности σ2 и объёма выборки n. Стандартная ошибка среднего вычисляется по формуле
![]()
где σ – величина среднеквадратического отклонения генеральной совокупности, и n – объём выборки. Поскольку дисперсия генеральной совокупности, как правило, неизвестна, то оценка стандартной ошибки вычисляется по формуле:
![]()
где s — стандартное отклонение случайной величины.
Сведем в одной таблице рассмотренные статистики:

Рис. 7. Рассмотренные статистики
Здесь в столбцах J:L приведены статистики для одной выборки размера n, а в столбце M – статистики для бутстрэп-выборок соответствующего размера с рис. 6. Если в Excel-файле на листе «Рис. 7» понажимать F9, вы увидите, что не всегда совпадение между столбцами L и M будет таким хорошим, но тенденция будет прослеживаться.
Выше я писал, что мы исследуем неизвестное математическое ожидание генеральной совокупности μ на основе среднего арифметического выборки X̅(100) = 0,119.
Мы можем использовать статистику, именуемую стандартной ошибкой. Для нас она черный ящик – формула, выведенная на основе теории вероятностей. С другой стороны мы можем построить множество бутстрэп-выборок размера n = 100, и подсчитать стандартное отклонение средних этих бутстрэп-выборок. И мы показали, что стандартная ошибка для одной выборки и стандартное отклонение средних бутстрэп-выборок, это одно и то же! В нашем примере, получив X̅(100) = 0,119, мы можем сказать, что с вероятностью 95% математическое ожидание генеральной совокупности μ лежит в диапазоне 0,119 ± 0,212 (0,106*2=0,212). Итак
стандартная ошибка – мера оценки математического ожидания генеральной совокупности μ на основании статистик выборки
Например, 95%-ный доверительный интервал для μ
Понятно, что с увеличением размера выборки n доверительный интервал будет сужаться. В пределе при n → ∞, X̅ → μ и SE → 0.
